题目内容
如图，在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C（C所在航线靠近A），直线l1、l2间的距离CD=1.5km，点B在点A的南偏西30°方向上，且AB=6km，A在C的北偏东60°方向上．求巡逻艇C与塔A之间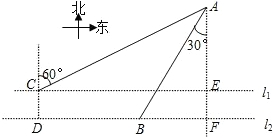
的距离AC．（结果精确到0.1km）（| 3 |
分析：此题可先由AB及方向角南偏西30°得出AF的长，再减去CD的长得AE的长，又A在C的北偏东60°方向上，得出AC的长．
解答：解：由题意可得：四边形CDFE是矩形，故EF=CD=1.5km（1分）
在Rt△ABF中，cos30°=
∴AF=ABcos30°=6×
=3
（3分）
∴AE=AF-EF=3
-1.5（4分）
在Rt△ABF中，∠ACE=30°
∴sin30°=
，即AC=
=2(3
-1.5)=6
-3≈7.4km（6分）
答：巡逻艇C与塔A之间的距离为7.4km（7分）
在Rt△ABF中，cos30°=
| AF |
| AB |
∴AF=ABcos30°=6×
| ||
| 2 |
| 3 |
∴AE=AF-EF=3
| 3 |
在Rt△ABF中，∠ACE=30°
∴sin30°=
| AE |
| AC |
| AE |
| sin30° |
| 3 |
| 3 |
答：巡逻艇C与塔A之间的距离为7.4km（7分）
点评：本题主要考查了方向角的含义，正确记忆三角函数的定义是解决本题的关键．
练习册系列答案
小学教材全测系列答案
相关题目
的距离AC．（结果精确到0.1km）（
）
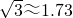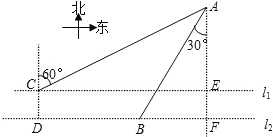
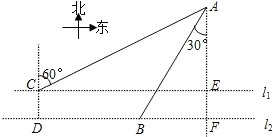如图，在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C（C所在航线靠近A），直线l1、l2间的距离CD=
km，点B在点A的南偏西30°方向上，且AB=6km，A在C的北偏东60°方向上．求：
） 
）