题目内容
4.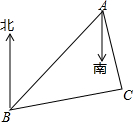 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向.
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向.(1)填空:∠BAS=45°;∠CAS=15°;∠CBN=80°;
(2)求∠ACB的度数.
分析 (1)根据方向角的定义,即可求得∠BAS,∠CAS,∠CBN的度数,
(2)根据三角形内角和定理即可求解.
解答 解:(1)如图,
∵B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,
∴∠BAS=45°,∠CAS=15°,∠CBN=80°,
故答案为:45,15,80°;
(2)∵AS,BN是正南正北方向,
∴BN∥AS,
∵∠BAS=45°,
∴∠NBA=∠BAS=45°,
∵∠NBC=80°,
∴∠ABC=80°-45°=35°,
∴∠ACB=180°-∠ABC-∠BAC=180°-60°-35°=85°.
点评 本题主要考查了方向角的定义,以及三角形的内角和定理,正确理解定义是解题的关键.

练习册系列答案
相关题目
19. 如图,△ABC中,∠A=80°,∠B=60°,则∠ACD的度数是( )
如图,△ABC中,∠A=80°,∠B=60°,则∠ACD的度数是( )
 如图,△ABC中,∠A=80°,∠B=60°,则∠ACD的度数是( )
如图,△ABC中,∠A=80°,∠B=60°,则∠ACD的度数是( )| A. | 60° | B. | 80° | C. | 100° | D. | 140° |
9.要使分式$\frac{1}{3-x}$有意义,则( )
| A. | x≠3 | B. | x=3 | C. | x>3 | D. | x>-3 |
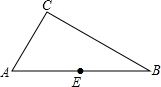 如图,△ABC中,∠CAB=60°,∠B=30°,E是AB的中点.
如图,△ABC中,∠CAB=60°,∠B=30°,E是AB的中点.