题目内容
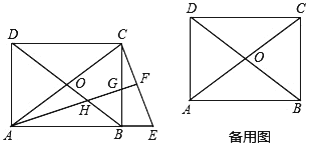
【题目】如图，在矩形
中，
，
，对角线
、
交于点
，点
在
延长线上，联结
，
，
分别交线段、边
、对角线于点
、
、
（点不与点
、重合）．
（1）当点是线段的中点，求
的长；
（2）设
，
，求
关于x的函数解析式，并写出它的定义域；
（3）当
是等腰三角形时，求
的长．
【答案】（1）
；（2）
；（3）
或
．
【解析】
（1）首先利用勾股定理得出
的长，证得
，得出
，进一步得出
，
，利用三角形相似的性质得出
、
的长，利用勾股定理求得而答案即可；
（2）作
，
，垂足分别为
、
，利用
，
，
，建立
、
之间的联系，进一步整理得出
关于x的函数解析式，根据
，得出x的定义域即可；
（3）分三种情况探讨：①当
时，②当
，③当
，分别探讨得出答案即可．
（1）
，
，∠ABC=90°，
，
，
，
点
是线段
的中点，
，
在
和
中，
，
，
，
，
，
，
，
，
，
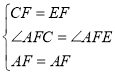
即
，
，
，
，
，
，
，
又
，
，
，
；
（2）如图，
作，，垂足分别为、，
，
，
，，，
，
，
，
，
又
，
，
，
，
，
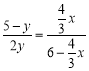则．
（3）当
是等腰三角形，
①当时，
，
，则
，
，由
，解得
；
②当，
，同理解得
；
③当，得出
不存在．
所以或．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为弘扬泰山文化，某校举办了“泰山诗文大赛”活动，从中随机抽取部分学生的比赛成绩，根据成绩（成绩都高于50分），绘制了如下的统计图表（不完整）：
组别 | 分数 | 人数 |
第1组 | 90＜x≤100 | 8 |
第2组 | 80＜x≤90 | a |
第3组 | 70＜x≤80 | 10 |
第4组 | 60＜x≤70 | b |
第5组 | 50＜x≤60 | 3 |
请根据以上信息，解答下列问题：
（1）求出a，b的值；
（2）计算扇形统计图中“第5组”所在扇形圆心角的度数；
（3）若该校共有1800名学生，那么成绩高于80分的共有多少人？
