题目内容
20．因式分解：（1）49（a-b）2-42（a-b）x+9x2=（7a-7b-3x）2．
（2）（a+2b）2+10（a+2b）+25=（a+2b+5）2．
（3）-5a3+10a2-5a=-5a（a-1）2．
（4）a4+2a2b2+b4=（a2+b2）2．
分析 （1）原式利用完全平方公式分解即可；
（2）原式利用完全平方公式分解即可；
（3）原式提取-5a，再利用完全平方公式分解即可；
（4）原式利用完全平方公式分解即可．
解答 解：（1）（1）49（a-b）2-42（a-b）x+9x2=（7a-7b-3x）2；
（2）（a+2b）2+10（a+2b）+25=（a+2b+5）2；
（3）-5a3+10a2-5a=-5a（a-1）2；
（4）a4+2a2b2+b4=（a2+b2）2．
故答案为：（1）（7a-7b-3x）2；（2）（a+2b+5）2；（3）-5a（a-1）2；（4）（a2+b2）2
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
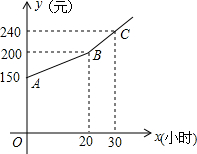为了鼓励小强做家务，小强每月的生活总费用都是由基本生活费和上月根据他的家务劳动时间所获得的奖励两部分组成．若设小强每月的家务劳动时间为x小时．下月他可获得的生活总费用为y元，則y（元）和x（小时）之间的函数图象如图所示．
11．某鞋业销售商在进行市场调查时，他最应该关注鞋子型号的（ ）
| A． | 平均数 | B． | 极差 | C． | 中位数 | D． | 众数 |
9．-$\frac{1}{3}$的相反数是（ ）
| A． | 3 | B． | -3 | C． | $\frac{1}{3}$ | D． | -$\frac{1}{3}$ |
