Question

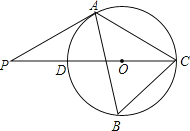
【题目】已知⊙O的直径AB＝4，⊙D与半径为1的⊙C外切，且⊙C与⊙D均与直径AB相切、与⊙O内切，那么⊙D的半径是_____．

Answer 1

【答案】或1

【解析】

分⊙D与⊙C在直径AB的同侧、⊙D与⊙C在直径AB的两侧两种情况，根据圆心距与两圆半径的数量关系、勾股定理列方程计算，得到答案．

解：当⊙D与⊙C在直径AB的同侧时，作DH⊥OC于H，DN⊥OB于N，连接CD，连接OD并延长交⊙O于G，

设⊙D的半径为r，则OD＝2﹣r，CD＝1+r，

∵⊙O的直径AB＝4，⊙C的半径为1，⊙C与⊙O内切，

∴⊙C与⊙O内切于点O，

∴CO⊥AB，

∵CO⊥AB，DH⊥OC，DN⊥OB，

∴四边形HOND为矩形，

∴OH＝DN＝r，DH＝ON＝，

∴CH＝1﹣r，

在Rt△CDH中，CH2+DH2＝CD2，即(1﹣r)2+(2﹣r)2﹣r2＝(1+r)2，

解得，r＝，

当⊙D与⊙C在直径AB的两侧时，⊙C与⊙D的半径相等，都是1，

故答案为：或1．