题目内容
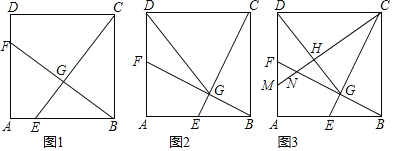
【题目】在边长为2的菱形ABCD中,E是边AD的中点,点F、G、H分别在边AB、BC、CD上,且FG⊥EF,EH⊥EF.
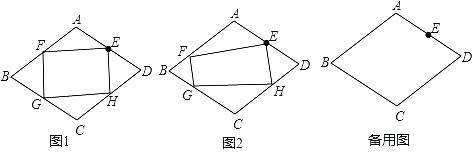
(1)如图1,当点![]() 是边
是边![]() 中点时,求证:四边形
中点时,求证:四边形![]() 是矩形;
是矩形;
(2)如图2,当![]() 时,求
时,求![]() 值;
值;
(3)当![]() ,且四边形
,且四边形![]() 是矩形时(点
是矩形时(点![]() 不与
不与![]() 中点重合),求
中点重合),求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)连接![]() 、
、![]() ,由菱形的性质及三角形的中位线定理证得
,由菱形的性质及三角形的中位线定理证得![]() ,
,![]() ,从而可知四边形
,从而可知四边形![]() 是平行四边形,再由有一个角为直角的平行四边形是矩形得出结论;
是平行四边形,再由有一个角为直角的平行四边形是矩形得出结论;
(2)连接![]() ,由菱形的性质及
,由菱形的性质及![]() 可得
可得![]() ,及
,及![]() ,从而判定
,从而判定![]() ,结合
,结合![]() 及菱形的性质可得答案;
及菱形的性质可得答案;
(3)如图,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 延长线于点
延长线于点![]() ,根据
,根据![]() 及菱形的边长可求得
及菱形的边长可求得![]() ,
,![]() .设
.设![]() ,则
,则![]() ,当四边形
,当四边形![]() 是矩形时,
是矩形时,![]() ,则
,则![]() 与
与![]() 相似(三垂直模型),分两种情况列式计算即可:①
相似(三垂直模型),分两种情况列式计算即可:①![]() ,②
,②![]() .
.
解:(1)连接![]() 、
、![]() ,
,

![]() 菱形
菱形![]() 中,
中,![]() 是边
是边![]() 的中点,点
的中点,点![]() 是边
是边![]() 中点,
中点,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形;
是矩形;
(2)连接![]() ,
,

![]() 菱形
菱形![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() 菱形
菱形![]() 中,
中,![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ;
;
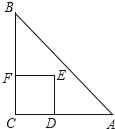
(3)如图,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 延长线于点
延长线于点![]() ,
,

![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() 由(2)可知,
由(2)可知,![]() ,
,
![]() 此时
此时![]() ,
,
又![]() 菱形
菱形![]() 边长为2,
边长为2,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设![]() ,则
,则![]() ,
,
当四边形![]() 是矩形时,
是矩形时,![]() ,则
,则![]() 与
与![]() 相似(三垂直模型).
相似(三垂直模型).
①若![]() ,
,
则![]() ,
,
![]()
 ,
,
解得![]() ,
,![]() (点
(点![]() 不与
不与![]() 中点重合,舍去);
中点重合,舍去);
②若![]() ,
,
则![]() ,
,
![]()
 ,
,
解得![]() .
.
综上,![]() 的长为
的长为![]() 或
或![]() .
.

练习册系列答案
相关题目