题目内容
 如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.(结果保留根号)
如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向的D处时,求此时轮船与灯塔C的距离.(结果保留根号)
分析:根据三角形外角和定理可求得BC的值,然后放到直角三角形BCD中,借助60°角的正弦值即可解答.
解答:解:由题意得∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
∴BC=BA=40海里,
∵∠CDB=90°,
∴sin∠CBD=
.
∴sin60°=
=
.
∴CD=BC×
=40×
=20
(海里).
∴此时轮船与灯塔C的距离为20
海里.
∴∠ACB=30°,
∴BC=BA=40海里,
∵∠CDB=90°,
∴sin∠CBD=
| CD |
| BC |
∴sin60°=
| CD |
| BC |
| ||
| 2 |
∴CD=BC×
| ||
| 2 |
| ||
| 2 |
| 3 |
∴此时轮船与灯塔C的距离为20
| 3 |
点评:将已知条件和所求结论转化到同一个直角三角形中求解是解直角三角形的常规思路.

练习册系列答案
相关题目
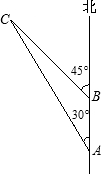 如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么?
如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么?

 如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么?
如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么? .
. .
.