题目内容
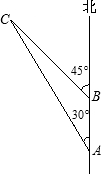 如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么?(
如图,一艘轮船以每分钟240米的速度向正北方向航行,行驶到A处测一灯塔C在它的北偏西30°的小岛上,轮船继续向北航行,5分钟后到达B点,又测得灯塔C在它的北偏西45°方向上.据有关资料记载,在距灯塔C为中心1500米范围内有暗礁.这艘轮船不改变前进方向继续行驶是否有触礁的危险?为什么?(| 3 |
分析:过点C作CE⊥AB于E.首先根据路程=速度×时间求得AB的长,设CE为x米.根据解直角三角形的知识分别用x表示BE和AE的长,从而列方程求得x的值,再进一步根据在距灯塔C为中心1500米范围内有暗礁进行比较判断.
解答: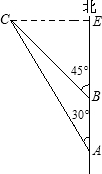 解:轮船不会触礁. (2分)
解:轮船不会触礁. (2分)
根据题意,得AB=240×5=1200.(3分)
设CE为x米.
过点C作CE⊥AB于E. (4分)
∵∠CBE=45度,
∴∠ECB=45度.
∴BE=CE=x.(5分)
∵∠CAE=30度,
∴tan30°=
,(6分)
∴
=
,(7分)
∴x=600(
+1)≈1639(米),(9分)
1639>1500,
故不会触礁. (10分)
 解:轮船不会触礁. (2分)
解:轮船不会触礁. (2分)根据题意,得AB=240×5=1200.(3分)
设CE为x米.
过点C作CE⊥AB于E. (4分)
∵∠CBE=45度,
∴∠ECB=45度.
∴BE=CE=x.(5分)
∵∠CAE=30度,
∴tan30°=
| CE |
| AE |
∴
| x |
| x+1200 |
| 1 | ||
|
∴x=600(
| 3 |
1639>1500,
故不会触礁. (10分)
点评:此题考查了解直角三角形的知识和垂线段最短的性质,要熟悉特殊角的锐角三角函数值.

练习册系列答案
相关题目



