题目内容
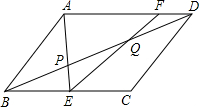如图，P、Q为平行四边形ABCD对角线BD上的三等分点，AP交BC于点E，EQ交AD于点F，则AF：FD=________．
3：1
分析：由四边形ABCD是平行四边形，可得AD∥BC，AD=BC，即可证得△BPE∽△DPA，△BQE∽△DQF，然后由相似三角形的对应边成比例，即可求得AF：FD的值．
解答：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△BPE∽△DPA，△BQE∽△DQF，
∴
，
，
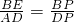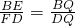∵P、Q为平行四边形ABCD对角线BD上的三等分点，
∴
，
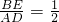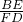=2，
∴FD：AD=1：4，
∴AF：FD=3：1．
故答案为：3：1．
点评：此题考查了相似三角形的判定与性质以及平行四边形的性质．此题难度适中，注意掌握数形结合思想的应用．
分析：由四边形ABCD是平行四边形，可得AD∥BC，AD=BC，即可证得△BPE∽△DPA，△BQE∽△DQF，然后由相似三角形的对应边成比例，即可求得AF：FD的值．
解答：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△BPE∽△DPA，△BQE∽△DQF，
∴
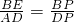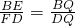，，∵P、Q为平行四边形ABCD对角线BD上的三等分点，
∴
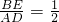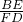，=2，∴FD：AD=1：4，
∴AF：FD=3：1．
故答案为：3：1．
点评：此题考查了相似三角形的判定与性质以及平行四边形的性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
20、如图，把边长为2cm的正方形剪成四个大小、形状完全一样的直角三角形．请用这四个直角三角形拼成符合下列要求的图形（全部用上，互不重叠且不留空隙），并把你的拼法画图示意：
空隙），把你的拼法画示意图（各画一个图即可），并求出它的周长：
16、如图，把边长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形拼成符合下列要求的图形．（全部用上，互不重合且不留空隙），并把你的拼法依照图示按实际大小画在方格内（方格为1cm×1cm）
19、如图，把边长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形画出符合下列要求的图形（注意：四个三角形要全部用上，互不重叠且不留空隙）．