题目内容
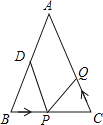
【题目】如图，在△ABC中，DE∥BC，EF∥AB，若S△ADE=16cm2，S△EFC=49cm2， 求①
，②S△ABC．
【答案】（1）
；（2）121
【解析】
利用平行求相似三角形，再根据相似三角形的性质，对应求解.
①∵DE∥BC，EF∥AB；
∴∠ADE=∠ABC, ∠AED=∠ACF；∴ΔADE∽ΔABC；
∠ABC=∠EFC, ∠EFC=∠ADE；∴ΔADE∽ΔEFC；
∴S△ADE：S△EFC =(BC：EF) =16:49, BC：EF=4：7；
∵DE∥BC，EF∥AB；
∴四边形DEFB为平行四边形，DE=BF；
∴
= .
②∵ΔADE∽ΔABC，= ；
∴S△ADE：S△ABC=（4:11）=16：121；
∵S△ADE=16cm2；
∴S△ABC E=121 cm2．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
