题目内容
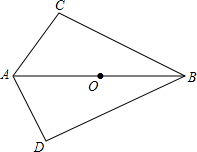 如图,在△ABC中,∠C=90°,AB的中点为O,
如图,在△ABC中,∠C=90°,AB的中点为O,(1)求证:A、B、C三点在以O为圆心,AB长为直径的圆上;
(2)若∠ADB=90°,求证:A,B,C,D四点在以O为圆心,AB为直径的圆上.
考点:直角三角形斜边上的中线
专题:证明题
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得OC=OA=OB,再根据圆的定义证明;
(2)根据直角三角形斜边上的中线等于斜边的一半可得OD=OA=OB=OC,然后判断出A、B、C、D四点共圆,再根据A、O、B三点共线证明即可.
(2)根据直角三角形斜边上的中线等于斜边的一半可得OD=OA=OB=OC,然后判断出A、B、C、D四点共圆,再根据A、O、B三点共线证明即可.
解答:(1)证明:∵∠C=90°,AB的中点为O,
∴OC=OA=OB,
∴A、B、C三点在以O为圆心,AB长为直径的圆上;
(2)解:∵∠ADB=90°,AB的中点为O,
∴OD=OA=OB=OC,
∴A、B、C、D四点共圆,
∵AB的中点为O,
∴A、O、B三点共线,
∴A,B,C,D四点在以O为圆心,AB为直径的圆上.
∴OC=OA=OB,
∴A、B、C三点在以O为圆心,AB长为直径的圆上;
(2)解:∵∠ADB=90°,AB的中点为O,
∴OD=OA=OB=OC,
∴A、B、C、D四点共圆,
∵AB的中点为O,
∴A、O、B三点共线,
∴A,B,C,D四点在以O为圆心,AB为直径的圆上.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,圆的定义,是基础题,熟记性质是解题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
某市2014年元旦的最高气温为4℃,最低气温为-7℃,那么,这天的最高气温比最低气温高( )
| A、3° | B、-3° |
| C、11° | D、-11° |
下列运算结果是负数的是( )
| A、(-5)+(-5) |
| B、(-5)-(-5) |
| C、(-5)*(-5) |
| D、(-5)÷(-5) |
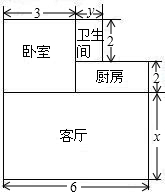 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题: 如图所示,根据图中信息,判断下列问题:
如图所示,根据图中信息,判断下列问题: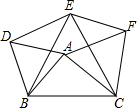 如图,已知△ABD,△BCE,△ACF都是等边三角形,试判断四边形ADEF的形状并说明理由.
如图,已知△ABD,△BCE,△ACF都是等边三角形,试判断四边形ADEF的形状并说明理由.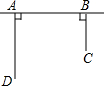 如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等.
如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等.