题目内容
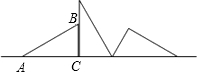
 如图,把Rt△ABC(∠C=90°)绕C点按顺时针的方向旋转α度后到△DEC的位置,若∠B=35°,∠1=25°,那么旋转角α等于________.
如图,把Rt△ABC(∠C=90°)绕C点按顺时针的方向旋转α度后到△DEC的位置,若∠B=35°,∠1=25°,那么旋转角α等于________.
25°
分析:根据旋转的性质可知△ABC≌△DEC,那么∠E=∠B,旋转角α即∠ACD,∠ACD+∠BCD=∠BCE+∠BCD,可得∠ACD=∠BCE,再由对顶角相等,∠E=∠B,所以得∠BCE=∠1=25°,从而求出旋转角α.
解答:如图,∵△ABC≌△DEC,
∴∠E=∠B,
∠ACB=∠DCE,
即∠ACD+∠BCD=∠BCE+∠BCD,
∴∠ACD=∠BCE,
再由对顶角相等和∠E=∠B,
∴∠BCE=∠1=25°,
所以α=∠ACD=∠BCE=25°,
故答案为:25°.
点评:本题考查了旋转的性质、全等三角形的判定和性质,解题的关键是知道一个图形旋转后得到的图形和原图形全等.
分析:根据旋转的性质可知△ABC≌△DEC,那么∠E=∠B,旋转角α即∠ACD,∠ACD+∠BCD=∠BCE+∠BCD,可得∠ACD=∠BCE,再由对顶角相等,∠E=∠B,所以得∠BCE=∠1=25°,从而求出旋转角α.
解答:如图,∵△ABC≌△DEC,
∴∠E=∠B,
∠ACB=∠DCE,
即∠ACD+∠BCD=∠BCE+∠BCD,
∴∠ACD=∠BCE,
再由对顶角相等和∠E=∠B,
∴∠BCE=∠1=25°,
所以α=∠ACD=∠BCE=25°,
故答案为:25°.
点评:本题考查了旋转的性质、全等三角形的判定和性质,解题的关键是知道一个图形旋转后得到的图形和原图形全等.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,把Rt△ABC依次绕顶点沿水平线翻转两次,若∠C=90°,AC=
如图,把Rt△ABC依次绕顶点沿水平线翻转两次,若∠C=90°,AC=| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( ) (2013•保康县模拟)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=6,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线
(2013•保康县模拟)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=6,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线 (2012•唐山二模)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为
(2012•唐山二模)如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为 (2012•郑州模拟)如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,sin∠C=0.6,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
(2012•郑州模拟)如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,sin∠C=0.6,点A、B的坐标分别为(2,0),(8,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )