Question

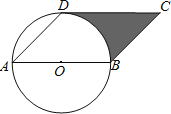
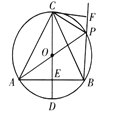
【题目】如图，在中，直径垂直弦于点，且.点为上一点（点不与点，重合），连结，，，，.过点作于点.给出下列结论:①是等边三角形；②在点从的运动过程中，的值始终等于.则下列说法正确的是（ ）

A.①，②都对B.①对，②错C.①错，②对D.①，②都错

Answer 1

【答案】A

【解析】

①根据OE=DE=OD，OE⊥AE,可得∠OAE=30°，再根据等腰三角形的性质，垂径定理的推论，可以得出△ABC中两个内角为60°，可以得出结论；②延长CP，使PQ=CP，连接BQ,根据∠BPQ=∠CAB=60°，可得△BPQ为等边三角形，再证明△CBQ≌△ABP，推出CQ=AP,因此AP-BP=CQ-PQ=CP,在Rt△CFP中从而可得出结论.

解：①∵OE=DE=OD，OE⊥AE,∴∠OAE=30°，

∴∠AOE=60°，又OC=AO,∴∠CAO=∠ACO=30°，

根据垂径定理的推论可得，弧AD=弧BD，∴∠ACD=∠BCD=30°，

∴∠CAB=∠ACB=60°，

∴△ABC为等边三角形.故①正确.

②延长CP，使PQ=CP，连接BQ,

∵四边形ABPC为圆O的内接圆，

∴∠BPQ=∠CAB=60°，

∴△BPQ为等边三角形，

∴BQ=BP=PQ，∠QBP=60°，

∴∠QBP=∠ABC,

∴∠CBQ=∠ABP，

又∠PAB=∠BCP,BQ=BP,

∴△CBQ≌△ABP（AAS）,

∴AP=CQ,

∴AP-BP=CQ-PQ=CP.

在Rt△CPF中，∠CPF=∠BPQ=60°，

∴,

∴

故②正确

故选：A.