题目内容
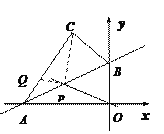
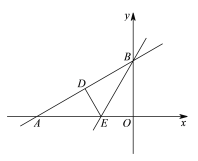
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
与x轴交于点A,与y轴交于点B.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
(1)求直线BE的解析式;
(2)求点D的坐标;
【答案】(1)直线BE的解析式为y=![]() x+2
x+2![]() ;(2)D(-3,
;(2)D(-3,![]() ).
).
【解析】
(1)先求出点A、B的坐标,继而根据勾股定理求出AB的长,根据折叠可得BD=BO,DE=OE,从而可得AD的长,设DE=OE=m,则AE=OA-m,在直角三角形AED中利用勾股定理求出m,从而得点E坐标,继而利用待定系数法进行求解即可;
(2)过点D作DM⊥AO,垂足为M,根据三角形的面积可求得DM的长,继而可求得点D的坐标.
(1)![]() ,令x=0,则y=2
,令x=0,则y=2![]() ,
,
令y=0,则![]() ,解得:x=-6,
,解得:x=-6,
∴A(-6,0),B(0,2![]() ),
),
∴OA=6,OB=2![]() ,
,
∴AB=![]() =4
=4![]() ,
,
∵折叠,
∴∠BDE=∠BOA=90°,DE=EO,BD=BO=2![]() ,
,
∴∠ADE=90°,AD=AB-BD=2![]() ,
,
设DE=EO=m,则AE=AO-OE=6-m,
在Rt△ADE中,AE2=AD2+DE2,
即(6-m)2=m2+(2![]() )2,
)2,
解得:m=2,
∴OE=2,
∴E(-2,0),
设直线BE的解析式为:y=kx+b,
把B、E坐标分别代入得: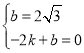 ,
,
解得: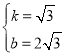 ,
,
∴直线BE的解析式为y=![]() x+2
x+2![]() ;
;
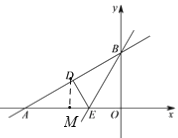
(2)过点D作DM⊥AO,垂足为M,
由(1)DE=2,AE=AO-OE=4,
∵S△ADE=![]() ,
,
即![]() ,
,
∴DM=![]() ,
,
∴点D的纵坐标为![]() ,
,
把y=![]() 代入
代入![]() ,得
,得
![]() ,
,
解得:x=-3,
∴D(-3,![]() ).
).

【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?