Question

【题目】在中，．

（1）观察猜想

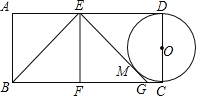
如图1，分别交于点的值是 ，直线与直线相交所成的较小角的度数是 ．

（2）类比探究

如图2，将绕点逆时针旋转，请写出的值及直线与直线相交所成的小角的度数，并就图2的情形说明理由，

（3）解决问题

若，请直接写出点在同一直线上时的值．

Answer 1

【答案】（1），45°；（2），直线BD与直线CP相交成小角的度数为45°，理由见解析；（3）或

【解析】

（1）由推出，变形即可求出，由已知条件中，，知三角形是等腰直角三角形，即可推出直线与直线相交所成的较小角的度数；

（2） 如图2中，假设BD与AC相交于点M，与PC交于点N，证明△PAC∽△DAB，即可解决问题；

（3）分两种情况：当点D在线段PC上时，当点P在线段CD上时，求解即可.

(1) ∵，

∴是等腰直角三角形，

∴直线与直线相交所成的较小角是∠A，∠A=45°，

∵，

∴，

∴，

∴；

(2)如图2中，设BD交AC于点O，BD交PC于点E．

∵∠PAD＝∠CAB＝45°，

∴∠PAC＝∠DAB，

∵，

∴，

∴△DAB∽△PAC，

∴∠PCA＝∠DBA，，

∵∠EOC＝∠AOB，

∴∠CEO＝∠OAB＝45°，

∴直线BD与直线CP相交所成的小角的度数为45°．

(3)或.

①如图，当点D在线段PC上时，

设PA＝PD＝1，则AC＝3，则PC＝，

∴，

∴；

②如图，当点P在线段CD上时，

设PA＝PD＝1，则AC＝3，则PC＝，

∴，

∴.

综上，的值为或.