题目内容
 如图,把△ABC纸片的∠A沿DE折叠,点A落在四边形CBDE外,则∠1、∠2与∠A的关系是( )
如图,把△ABC纸片的∠A沿DE折叠,点A落在四边形CBDE外,则∠1、∠2与∠A的关系是( )| A、∠1+∠2=2∠A | ||
| B、∠2-∠A=2∠1 | ||
| C、∠2-∠1=2∠A | ||
D、∠1+∠A=
|
分析:如图,分别延长CEBD交于A′点,然后利用三角形的外角与内角的关系可以得到∠2=∠EA′A+∠EAA′,∠1=∠DA′A+∠DAA′,而根据折叠可以得到∠EA′A=∠EAA′,∠DA′A=∠DAA′,然后利用等式的性质即可求解.
解答: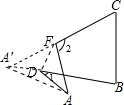 解:如图:分别延长CE、BD交于A′点,
解:如图:分别延长CE、BD交于A′点,
∴∠2=∠EA′A+∠EAA′,∠1=∠DA′A+∠DAA′,
而根据折叠可以得到∠EA′A=∠EAA′,∠DA′A=∠DAA′,
∴∠2-∠1=2(∠EAA′-∠DAA′)=2∠EAD.
故选C.
 解:如图:分别延长CE、BD交于A′点,
解:如图:分别延长CE、BD交于A′点,∴∠2=∠EA′A+∠EAA′,∠1=∠DA′A+∠DAA′,
而根据折叠可以得到∠EA′A=∠EAA′,∠DA′A=∠DAA′,
∴∠2-∠1=2(∠EAA′-∠DAA′)=2∠EAD.
故选C.
点评:本题考查图形的折叠与拼接,同时考查了三角形、四边形等几何基本知识,解题时应分别对每一个图形进行仔细分析,难度不大.

练习册系列答案
相关题目
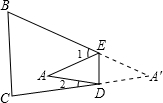 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,

 20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是
20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,