题目内容
阅读理解:对于任意正实数a、b,∵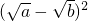 ≥0,∴
≥0,∴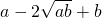 ≥0,∴a+b≥
≥0,∴a+b≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在a+b≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 .
.
根据上述内容,回答下列问题:
(1)若m>0,只有当m=______时,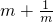 有最小值 ______.
有最小值 ______.
(2)若m>0,只有当m=______时,2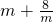 有最小值 ______.
有最小值 ______.
解:(1)当m= 时,则m2=1,
时,则m2=1,
解得m=±1,
∵m>0,
∴m=1,
∴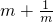 有最小值是2;
有最小值是2;
(2)当2m= 时,则m2=4,
时,则m2=4,
解得m=±2,
∵m>0,
∴m=2,
∴2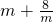 有最小值8.
有最小值8.
故答案为:2;8.
分析:根据已知条件,(1)当m= 时,
时,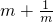 有最小值2
有最小值2 ;(2)同理,当2m=
;(2)同理,当2m= 时,2
时,2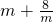 有最小值2
有最小值2 ;从而得出答案.
;从而得出答案.
点评:本题是一个阅读材料题,考查了反比例函数的性质,是中考压轴题,难度较大.
 时,则m2=1,
时,则m2=1,解得m=±1,
∵m>0,
∴m=1,
∴
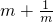 有最小值是2;
有最小值是2;(2)当2m=
 时,则m2=4,
时,则m2=4,解得m=±2,
∵m>0,
∴m=2,
∴2
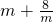 有最小值8.
有最小值8.故答案为:2;8.
分析:根据已知条件,(1)当m=
 时,
时,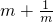 有最小值2
有最小值2 ;(2)同理,当2m=
;(2)同理,当2m= 时,2
时,2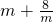 有最小值2
有最小值2 ;从而得出答案.
;从而得出答案.点评:本题是一个阅读材料题,考查了反比例函数的性质,是中考压轴题,难度较大.

练习册系列答案
相关题目
 问栏杆多少长时,所用拉力F最小?是多少?
问栏杆多少长时,所用拉力F最小?是多少? 阅读理解:对于任意正实数a,b,
阅读理解:对于任意正实数a,b,
 阅读理解:
阅读理解: