ΧβΡΩΡΎ»ί
 ‘ΡΕΝάμΫβΘΚΕ‘”Ύ»Έ“β’ΐ Β ΐaΘ§bΘ§
‘ΡΕΝάμΫβΘΚΕ‘”Ύ»Έ“β’ΐ Β ΐaΘ§bΘ§ΓΏΘ®
| a |
| b |
Γύa-2
| ab |
Γύa+bΓί2
| ab |
Ϋα¬έΘΚ‘Ύa+bΓί2
| ab |
| p |
Β±a=bΘ§a+b”–Ήν–Γ÷Β2
| p |
ΗυΨί…œ ωΡΎ»ίΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©»τxΘΨ0Θ§x+
| 4 |
| x |
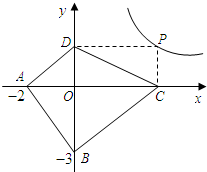
Θ®2Θ©ΧΫΥς”Π”ΟΘΚ»γΆΦΘ§“―÷ΣAΘ®-2Θ§0Θ©Θ§BΘ®0Θ§-3Θ©Θ§ΒψPΈΣΥΪ«ζœΏy=
| 6 |
| x |
Ζ÷ΈωΘΚΘ®1Θ©άϊ”Ο‘Ύa+bΓί2
ΒΟΒΫx+
Γί2
Θ§Φ¥Ω…ΒΟΒΫx+
ΒΡΉν–Γ÷ΒΘΜ
Θ®2Θ©…ηpΘ®xΘ§
Θ©Θ§‘ρCΘ®xΘ§0Θ©Θ§DΘ®0Θ§
Θ©Θ§‘ρΩ…±μ Ψ≥ωΥΡ±Ώ–ΈABCDΟφΜΐS=
AC•DB=
Θ®x+2Θ©Θ®
+3Θ©Θ§±δ–ΈΒΟS=
Θ®x+
Θ©+6Θ§άϊ”Ο«ΑΟφΒΡΫα¬έΩ…ΒΟΥΡ±Ώ–ΈABCDΟφΜΐΒΡΉν–Γ÷ΒΈΣ12Θ°¥Υ ±x=
Θ§‘ρx=2Θ§ΒΟΒΫOA=OC=2Θ§OD=OB=3Θ§άϊ”ΟΤΫ––ΥΡ±Ώ–ΈΒΡ≈–Ε®Ε®άμΩ…ΒΟΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘ§ΕχACΓΆBDΘ§‘ΌΗυΨίΝβ–ΈΒΡ≈–Ε®Ε®άμΒΟΒΫΥΡ±Ώ–ΈABCD «Νβ–ΈΘ°
| ab |
| 4 |
| x |
x•
|
| 4 |
| x |
Θ®2Θ©…ηpΘ®xΘ§
| 6 |
| x |
| 6 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| x |
| 3 |
| 2 |
| 4 |
| x |
| 4 |
| x |
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©4ΘΜ
Θ®2Θ©…ηPΘ®xΘ§
Θ©Θ§‘ρCΘ®xΘ§0Θ©Θ§DΘ®0Θ§
Θ©Θ§
ΓύΥΡ±Ώ–ΈABCDΟφΜΐS=
AC•DB=
Θ®x+2Θ©Θ®
+3Θ©
=
Θ®x+
Θ©+6Θ§
”…Θ®1Θ©ΒΟ»τxΘΨ0Θ§x+
ΒΡΉν–Γ÷ΒΈΣ4Θ§
ΓύΥΡ±Ώ–ΈABCDΟφΜΐSΓί
ΓΝ4+6=12Θ§
ΓύΥΡ±Ώ–ΈABCDΟφΜΐΒΡΉν–Γ÷ΒΈΣ12Θ°
¥Υ ±x=
Θ§‘ρx=2Θ§
ΓύCΘ®2Θ§0Θ©Θ§DΘ®0Θ§3Θ©Θ§
ΓύOA=OC=2Θ§OD=OB=3Θ§
ΓύΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘ°
”÷ACΓΆBDΘ§
ΓύΥΡ±Ώ–ΈABCD «Νβ–ΈΘ°
Θ®2Θ©…ηPΘ®xΘ§
| 6 |
| x |
| 6 |
| x |
ΓύΥΡ±Ώ–ΈABCDΟφΜΐS=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| x |
=
| 3 |
| 2 |
| 4 |
| x |
”…Θ®1Θ©ΒΟ»τxΘΨ0Θ§x+
| 4 |
| x |
ΓύΥΡ±Ώ–ΈABCDΟφΜΐSΓί
| 3 |
| 2 |
ΓύΥΡ±Ώ–ΈABCDΟφΜΐΒΡΉν–Γ÷ΒΈΣ12Θ°
¥Υ ±x=
| 4 |
| x |
ΓύCΘ®2Θ§0Θ©Θ§DΘ®0Θ§3Θ©Θ§
ΓύOA=OC=2Θ§OD=OB=3Θ§
ΓύΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘ°
”÷ACΓΆBDΘ§
ΓύΥΡ±Ώ–ΈABCD «Νβ–ΈΘ°
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥ‘ΡΕΝάμΫβΧβΒΡΫβΧβΖΫΖ®ΘΚάϊ”ΟΧβΡΩ÷–ΗχΒΡΖΫΖ®ΜρΫα¬έΫβΨωΈ ΧβΘ°“≤ΩΦ≤ιΝΥάϊ”ΟΉχ±ξ±μ ΨœΏΕΈ≥Λ“‘ΦΑΤΫ––ΥΡ±Ώ–ΈΚΆΝβ–ΈΒΡ≈–Ε®ΖΫΖ®Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 Έ άΗΗΥΕύ…Ό≥Λ ±Θ§Υυ”Οά≠ΝΠFΉν–ΓΘΩ «Εύ…ΌΘΩ
Έ άΗΗΥΕύ…Ό≥Λ ±Θ§Υυ”Οά≠ΝΠFΉν–ΓΘΩ «Εύ…ΌΘΩ
 ‘ΡΕΝάμΫβΘΚ
‘ΡΕΝάμΫβΘΚ