题目内容
已知:
=
-1,
=
-
,
=2-
,….
(1)请你用含n(n是正整数)的式子表示上面等式;
(2)计算
+
+…+
+
.
| 1 | ||
|
| 2 |
| 1 | ||||
|
| 3 |
| 2 |
| 1 | ||
2+
|
| 3 |
(1)请你用含n(n是正整数)的式子表示上面等式;
(2)计算
| 1 | ||
1+
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
分析:(1)根据所给特例,不难发现:
=
-
.根据这一性质即可化简.
(2)根据(1)的结论,化简各个二次根式,发现抵消的规律,计算出最后结果.
| 1 | ||||
|
| n+1 |
| n |
(2)根据(1)的结论,化简各个二次根式,发现抵消的规律,计算出最后结果.
解答:解:(1)
=
-
(n是正整数);
(2)解:原式=(
-1+
-
+…+
-
)
=
-1.
| 1 | ||||
|
| n+1 |
| n |
(2)解:原式=(
| 2 |
| 3 |
| 2 |
| 2011 |
| 2010 |
=
| 2011 |
点评:本题主要考查分母有理化的方法,解题关键是掌握二次根式分母有理化的方法,注意化简后抵消的规律.

练习册系列答案
相关题目
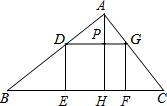 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.