题目内容
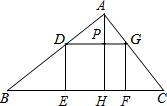 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.分析:根据矩形面积=长×宽,可以先设出未知数DE=x,再把另一边用x表示出来,求出面积表达式,再根据二次函数的性质求最大值即可.
解答:解:设DE=x,S矩形=y,
∵四边形DGFE是矩形,
∴DG∥BC,
∴△ADG∽△ABC,
∴
=
,
∵AP=AH-PH=AH-DE=8-x,BC=12,AH=8,
∴
=
,
∴DG=
(8-x),
∴y=DG•DE=
(8-x)x=12x-x2=-(x-6)2+36,
从而当x=6时,y有最大值36.此时矩形的宽为6,即四边形DGEF为正方形,
答:矩形DEFG的长和宽都是6.
∵四边形DGFE是矩形,
∴DG∥BC,
∴△ADG∽△ABC,
∴
| AP |
| AH |
| DG |
| BC |
∵AP=AH-PH=AH-DE=8-x,BC=12,AH=8,
∴
| 8-x |
| 8 |
| DG |
| 12 |
∴DG=
| 3 |
| 2 |
∴y=DG•DE=
| 3 |
| 2 |
从而当x=6时,y有最大值36.此时矩形的宽为6,即四边形DGEF为正方形,
答:矩形DEFG的长和宽都是6.
点评:本题考查了相似三角形的判定和性质、矩形的性质以及二次函数的应用,以及二次函数求最值的问题,只要能熟练掌握,便能很容易的解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
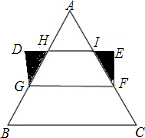 如图,矩形DEFG的一组对边DE、GF截等边三角形ABC的两边AB、AC均成三等分,点G、F分别在AB、AC上,已知图中两个三角形(阴影部分)的面积和为
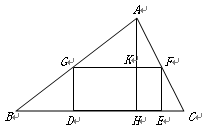
如图,矩形DEFG的一组对边DE、GF截等边三角形ABC的两边AB、AC均成三等分,点G、F分别在AB、AC上,已知图中两个三角形(阴影部分)的面积和为 (2012•崇明县一模)已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF:GF=1:2,求矩形DEFG的周长.
(2012•崇明县一模)已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF:GF=1:2,求矩形DEFG的周长.