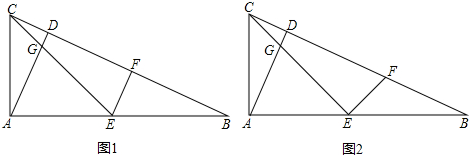
题目内容
（2013•绍兴）在平面直角坐标系中，O是原点，A是x轴上的点，将射线OA绕点O旋转，使点A与双曲线y=
上的点B重合，若点B的纵坐标是1，则点A的横坐标是
| ||
| x |
2或-2
2或-2
．分析：根据反比例函数的性质得出B点坐标，进而得出A点坐标．
解答：
解：如图所示：
∵点A与双曲线y=
上的点B重合，点B的纵坐标是1，
∴点B的横坐标是
，
∴OB=
=2，
∵A点可能在x轴的正半轴也可能在负半轴，
∴A点坐标为：（2，0），（-2，0）．
故答案为：2或-2．
解：如图所示：∵点A与双曲线y=
| ||
| x |
∴点B的横坐标是
| 3 |
∴OB=
12+(
|
∵A点可能在x轴的正半轴也可能在负半轴，
∴A点坐标为：（2，0），（-2，0）．
故答案为：2或-2．
点评：此题主要考查了勾股定理以及反比例函数的性质等知识，根据已知得出BO的长是解题关键．
练习册系列答案
相关题目
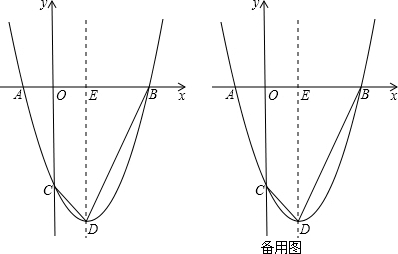
（2013•绍兴模拟）小刚在纸上画了一个面积为6分米2的正六边形，然后连接相隔一点的两点得到如图所示的对称图案，他发现中间也出现了一个正六边形，则中间的正六边形的面积是