题目内容
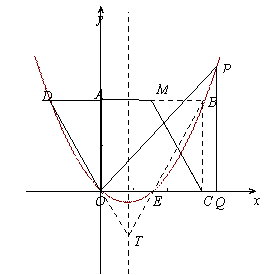
已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
(1)直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连结OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得![]() 的值最大.若存在,求出T点坐标;若不存在,请说明理由.
的值最大.若存在,求出T点坐标;若不存在,请说明理由.

解:
(1)依题意得:![]()
(2) ① ∵![]() ,
,![]() ,∴
,∴![]() .
.
∵抛物线经过原点,
∴设抛物线的解析式为![]()
![]()
又抛物线经过点![]() 与点
与点![]()
∴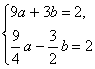 解得:
解得: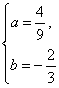
∴抛物线的解析式为![]() .
.
∵点![]() 在抛物线上,
在抛物线上,
∴设点![]() .
.
1)若![]() ∽
∽![]() ,则
,则![]() ,
, 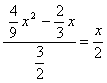
解得:![]() (舍去)或
(舍去)或![]() ,
,
∴点![]() .
.
 2)若
2)若![]() ∽
∽![]() ,则
,则![]() ,
, 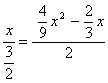 ,解得:
,解得:![]() (舍去)或
(舍去)或![]() ,
,
∴点![]()
②存在点![]() ,使得
,使得![]() 的值最大.
的值最大.
抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,设抛物线与
,设抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,则点
,则点![]() .
.
∵点![]() 、点
、点![]() 关于直线
关于直线![]() 对称,
对称,
∴![]()
要使得![]() 的值最大,即是使得
的值最大,即是使得![]() 的值最大,
的值最大,
根据三角形两边之差小于第三边可知,当![]() 、
、![]() 、
、![]() 三点在同一直线上时,
三点在同一直线上时,![]() 的值最大.设过
的值最大.设过![]() 、
、![]() 两点的直线解析式为
两点的直线解析式为![]()
![]() ,
,
∴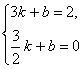 解得:
解得: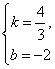
∴直线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]() .
.
∴存在一点![]() 使得
使得![]() 最大.
最大.

练习册系列答案
相关题目
 已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.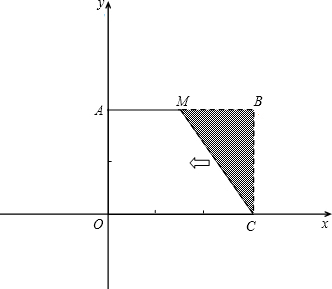 点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
点M,连接MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.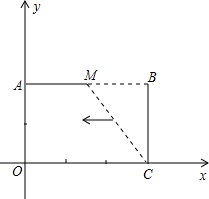 已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.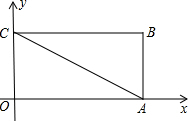 ,并且OC>OE.
,并且OC>OE.