Question

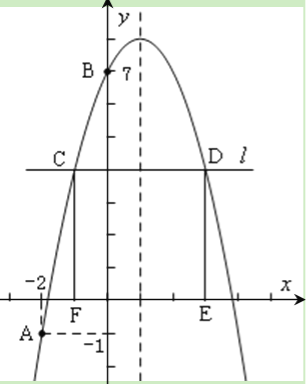
【题目】（11·永州）（本题满分10分）如图，已知二次函数的图象经过

A（，），B（0,7）两点．

⑴ 求该抛物线的解析式及对称轴；

⑵ 当为何值时，？

⑶ 在轴上方作平行于轴的直线，与抛物线交于C，D两点（点C在对称轴的左侧），

过点C，D作轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标．

Answer 1

【答案】解：⑴把A（，），B（0,7）两点的坐标代入，得

解得

所以，该抛物线的解析式为，

又因为，所以对称轴为直线．

⑵当函数值时，的解为，

结合图象，容易知道时，．

⑶当矩形CDEF为正方形时，设C点的坐标为（m，n），

则，即

因为C，D两点的纵坐标相等，所以C，D两点关于对称轴对称，设点D的横坐标为，则，所以，所以CD=

因为CD=CF，所以，整理，得，解得或5．

因为点C在对称轴的左侧，所以只能取．

当时，==4

于是，得点C的坐标为（，4）．

【解析】略