题目内容
直线y=kx与抛物线y=3-（x-2）2有公共点，则k的取值范围是________．
k≤2或k≥6
分析：由于直线y=kx与抛物线y=3-（x-2）2有公共点，由此得到由函数解析式组成的方程有实数解，然后利用判别式即可得到关于k的方程，解方程即可求解．
解答：∵直线y=kx与抛物线y=3-（x-2）2有公共点，
∴关于x的二次方程3-（x-2）2=kx，
即x2+（k-4）x+1=0有实数解．
故△=（k-4）2-4≥0，
∴k≤2或k≥6．
故答案为：k≤2或k≥6．
点评：此题主要考查了抛物线与直线的交点及一元二次方程的判别式，解题时首先根据直线与抛物线有交点利用判别式得到关于k的不等式，解表达式即可解决问题．
分析：由于直线y=kx与抛物线y=3-（x-2）2有公共点，由此得到由函数解析式组成的方程有实数解，然后利用判别式即可得到关于k的方程，解方程即可求解．
解答：∵直线y=kx与抛物线y=3-（x-2）2有公共点，
∴关于x的二次方程3-（x-2）2=kx，
即x2+（k-4）x+1=0有实数解．
故△=（k-4）2-4≥0，
∴k≤2或k≥6．
故答案为：k≤2或k≥6．
点评：此题主要考查了抛物线与直线的交点及一元二次方程的判别式，解题时首先根据直线与抛物线有交点利用判别式得到关于k的不等式，解表达式即可解决问题．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
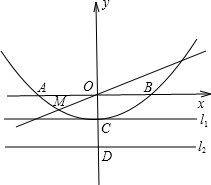（2012•潍坊）如图，已知抛物线与坐标轴分别交于A（-2，0），B（2，0），C（0，-1）三点，过坐标原点O的直线y=kx与抛物线交于M、N两点．分别过点C、D（0，-2）作平行于x轴的直线l1、l2．
于M、N两点．分别过点C,D(0，-2)作平行于x轴的直线
．
相切；
的距离之和等于线段MN的长．