题目内容
（2012•义乌市）如图1，已知直线y=kx与抛物线y=-
x2+
交于点A（3，6）．
（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？
| 4 |
| 27 |
| 22 |
| 3 |
（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？
分析：（1）利用待定系数法求出直线y=kx的解析式，根据A点坐标用勾股定理求出线段OA的长度；
（2）如答图1，过点Q作QG⊥y轴于点G，QH⊥x轴于点H，构造相似三角形△QHM与△QGN，将线段QM与线段QN的长度之比转化为相似三角形的相似比，即
=
=
=tan∠AOM=2为定值．需要注意讨论点的位置不同时，这个结论依然成立；
（3）由已知条件角的相等关系∠BAE=∠BED=∠AOD，可以得到△ABE∽△OED．设OE=a，则由相似边的比例关系可以得到m关于x的表达式m=-
a2+
a（0＜a＜3
），这是一个二次函数．借助此二次函数图象（如答图3），可见m在不同取值范围时，a的取值（即OE的长度，或E点的位置）有1个或2个．这样就将所求解的问题转化为分析二次函数的图象与性质问题．
另外，在相似三角形△ABE与△OED中，运用线段比例关系之前需要首先求出AB的长度．如答图2，可以通过构造相似三角形，或者利用一次函数（直线）的性质求得AB的长度．
（2）如答图1，过点Q作QG⊥y轴于点G，QH⊥x轴于点H，构造相似三角形△QHM与△QGN，将线段QM与线段QN的长度之比转化为相似三角形的相似比，即
| QM |
| QN |
| QH |
| QG |
| QH |
| OH |
（3）由已知条件角的相等关系∠BAE=∠BED=∠AOD，可以得到△ABE∽△OED．设OE=a，则由相似边的比例关系可以得到m关于x的表达式m=-
| 1 |
| 5 |
3
| ||
| 5 |
| 5 |
另外，在相似三角形△ABE与△OED中，运用线段比例关系之前需要首先求出AB的长度．如答图2，可以通过构造相似三角形，或者利用一次函数（直线）的性质求得AB的长度．
解答：解：（1）把点A（3，6）代入y=kx 得；
∵6=3k，
∴k=2，
∴y=2x．（2分）
OA=
=3
．…（3分）
（2）
是一个定值，理由如下：
如答图1，过点Q作QG⊥y轴于点G，QH⊥x轴于点H．
①当QH与QM重合时，显然QG与QN重合，
此时
=
=
=tan∠AOM=2；
②当QH与QM不重合时，
∵QN⊥QM，QG⊥QH
不妨设点H，G分别在x、y轴的正半轴上，
∴∠MQH=∠GQN，
又∵∠QHM=∠QGN=90°
∴△QHM∽△QGN…（5分），
∴
=
=
=tan∠AOM=2，
当点P、Q在抛物线和直线上不同位置时，同理可得
=2． …（7分）①①
（3）如答图2，延长AB交x轴于点F，过点F作FC⊥OA于点C，过点A作AR⊥x轴于点R
∵∠AOD=∠BAE，
∴AF=OF，
∴OC=AC=
OA=
∵∠ARO=∠FCO=90°，∠AOR=∠FOC，
∴△AOR∽△FOC，
∴
=
=
=
，
∴OF=
×
=
，
∴点F（
，0），
设点B（x，-
x2+
），
过点B作BK⊥AR于点K，则△AKB∽△ARF，
∴
=
，
即
=
，
解得x1=6，x2=3（舍去），
∴点B（6，2），
∴BK=6-3=3，AK=6-2=4，
∴AB=5 …（8分）；
（求AB也可采用下面的方法）
设直线AF为y=kx+b（k≠0）把点A（3，6），点F（
，0）代入得
k=-
，b=10，
∴y=-
x+10，
∴
，
∴
（舍去），
，
∴B（6，2），
∴AB=5…（8分）
（其它方法求出AB的长酌情给分）
在△ABE与△OED中
∵∠BAE=∠BED，
∴∠ABE+∠AEB=∠DEO+∠AEB，
∴∠ABE=∠DEO，
∵∠BAE=∠EOD，
∴△ABE∽△OED．…（9分）
设OE=a，则AE=3
-a（0＜a＜3
），
由△ABE∽△OED得
=
，
∴
=
，
∴m=
a（3
-a）=-
a2+
a（0＜a＜3
），
∴顶点为（
，
）
如答图3，当m=
时，OE=a=
，此时E点有1个；
当0＜m＜
时，任取一个m的值都对应着两个a值，此时E点有2个．
∴当m=
时，E点只有1个…（11分）
当0＜m＜
时，E点有2个…（12分）．
∵6=3k，
∴k=2，
∴y=2x．（2分）
OA=
| 32+62 |
| 5 |
（2）
| QM |
| QN |
如答图1，过点Q作QG⊥y轴于点G，QH⊥x轴于点H．
①当QH与QM重合时，显然QG与QN重合，
此时
| QM |
| QN |
| QH |
| QG |
| QH |
| OH |
②当QH与QM不重合时，
∵QN⊥QM，QG⊥QH
不妨设点H，G分别在x、y轴的正半轴上，
∴∠MQH=∠GQN，
又∵∠QHM=∠QGN=90°
∴△QHM∽△QGN…（5分），
∴
| QM |
| QN |
| QH |
| QG |
| QH |
| OH |
当点P、Q在抛物线和直线上不同位置时，同理可得
| QM |
| QN |
（3）如答图2，延长AB交x轴于点F，过点F作FC⊥OA于点C，过点A作AR⊥x轴于点R
∵∠AOD=∠BAE，
∴AF=OF，
∴OC=AC=
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
∵∠ARO=∠FCO=90°，∠AOR=∠FOC，
∴△AOR∽△FOC，
∴
| OF |
| OC |
| AO |
| OR |
3
| ||
| 3 |
| 5 |
∴OF=
| 3 |
| 2 |
| 5 |
| 5 |
| 15 |
| 2 |
∴点F（
| 15 |
| 2 |
设点B（x，-
| 4 |
| 27 |
| 22 |
| 3 |
过点B作BK⊥AR于点K，则△AKB∽△ARF，
∴
| BK |
| FR |
| AK |
| AR |
即
| x-3 |
| 7.5-3 |
6-(-
| ||||
| 6 |
解得x1=6，x2=3（舍去），
∴点B（6，2），
∴BK=6-3=3，AK=6-2=4，
∴AB=5 …（8分）；
（求AB也可采用下面的方法）
设直线AF为y=kx+b（k≠0）把点A（3，6），点F（
| 15 |
| 2 |
k=-
| 4 |
| 3 |
∴y=-
| 4 |
| 3 |
∴
|
∴
|
|
∴B（6，2），
∴AB=5…（8分）
（其它方法求出AB的长酌情给分）
在△ABE与△OED中
∵∠BAE=∠BED，
∴∠ABE+∠AEB=∠DEO+∠AEB，
∴∠ABE=∠DEO，
∵∠BAE=∠EOD，
∴△ABE∽△OED．…（9分）
设OE=a，则AE=3
| 5 |
| 5 |
由△ABE∽△OED得
| AE |
| AB |
| OD |
| OE |
∴
3
| ||
| 5 |
| m |
| a |
∴m=
| 1 |
| 5 |
| 5 |
| 1 |
| 5 |
3
| ||
| 5 |
| 5 |
∴顶点为（
| 3 |
| 2 |
| 5 |
| 9 |
| 4 |
如答图3，当m=
| 9 |
| 4 |
| 3 |
| 2 |
| 5 |
当0＜m＜
| 9 |
| 4 |
∴当m=
| 9 |
| 4 |
当0＜m＜
| 9 |
| 4 |
点评：本题是中考压轴题，难度较大，解题核心是相似三角形与抛物线的相关知识，另外也考查了一次函数、勾股定理等重要知识点．解题的难点在于转化思想的运用，本题第（2），（3）问都涉及到了问题的转化，要求同学们能够将所求解的问题转化为常见的数学问题，利用自己所熟悉的数学知识去解决问题，否则解题时将不知道从何下手而导致失分．
练习册系列答案
精英口算卡系列答案
相关题目
（2012•义乌市）如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数
（2012•义乌市模拟）如图，DE是△ABC的中位线，DE=2cm，则BC=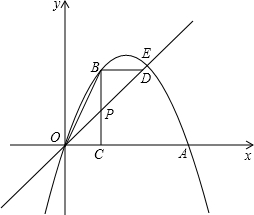
（2012•义乌市模拟）已知抛物线