题目内容
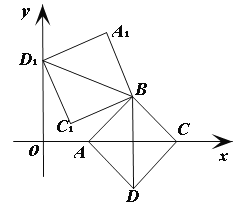
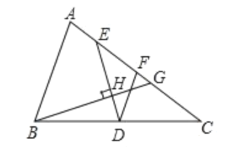
【题目】如图1.在![]() 中,
中,![]() 把
把![]() 沿对角线
沿对角线![]() 所在的直线折叠,使点
所在的直线折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .连接
.连接![]() .
.
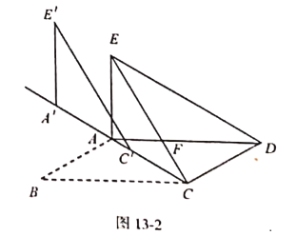
(1)求证:![]() ;
;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
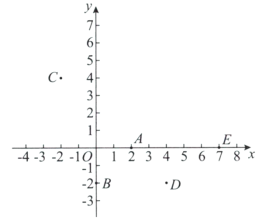
(3)将图1中![]() 的沿射线
的沿射线![]() 方向平移得到
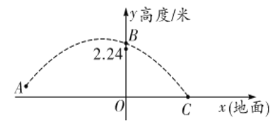
方向平移得到![]() (如图2所示) .若在
(如图2所示) .若在![]() 中,
中,![]() . 当
. 当![]() 时,直接写出
时,直接写出![]() 平移的距离.
平移的距离.
【答案】(1)详见解析;(2)详见解析;(3)4
【解析】
(1)利用平行四边形的性质及翻折的性质可知![]() ,又
,又![]() 即可证明
即可证明![]() ;
;
(2)由![]() 得到
得到![]() ,证得EF=FD,即可得到
,证得EF=FD,即可得到![]() 为等腰三角形;
为等腰三角形;
(3)过点A作AM⊥BC,先根据等腰三角形三线合一的性质及解直角三角形可得∠BAM=∠CAM=60°,得到∠BAN=60°,过点B作BN⊥AA![]() ,从而得到AN=1,BN=
,从而得到AN=1,BN=![]() ,在Rt
,在Rt![]() A
A![]() BN中,由勾股定理得
BN中,由勾股定理得![]() N=3,从而得到A A
N=3,从而得到A A![]() =4,因而平移的距离即为4.
=4,因而平移的距离即为4.
![]() 证明:
证明: ![]() 中,
中,
![]() .
.
由折叠可知:![]()
![]()
又![]()
![]()
![]() 证明:
证明:![]()
![]()
∴EF=FD
![]() 为等腰三角形
为等腰三角形
![]() ,理由如下:图形的平移距离即为对应点连续段的长度,如A A
,理由如下:图形的平移距离即为对应点连续段的长度,如A A![]() 的长度;
的长度;
如图,过点A作AM⊥BC,
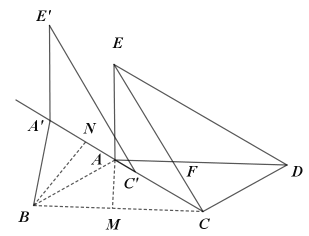
∵![]() ,
,
∴BM=CM=![]() ,∠BAM=∠CAM,
,∠BAM=∠CAM,
在Rt![]() BAM中,sin∠BAM=
BAM中,sin∠BAM=![]() ,
,
∴∠BAM=∠CAM=60°,
∴∠BAN=180°-∠BAM-∠CAM=60°
过点B作BN⊥AA![]() ,
,
在Rt![]() BAN中,∠BAN=60°,
BAN中,∠BAN=60°,
∴∠ABN=30°
∴AN=![]() ,
,
∴BN=AN×tan60°=![]() ,
,
在Rt![]() A
A![]() BN中,
BN中,![]() ,BN=
,BN=![]() ,由勾股定理得
,由勾股定理得
![]() N=
N=![]() ,
,
∴![]() =AN+
=AN+![]() N=1+3=4,
N=1+3=4,
故![]() 平移的距离为4个单位
平移的距离为4个单位

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目