题目内容
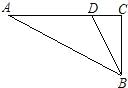如图，∠C=90°，∠ABC=75°，∠CBD=30°，若BC=3 cm，则AD=________cm．
6+
分析：由已知条件可知：BD=2CD，根据勾股定理可求出BD、CD，作AB的垂直平分线，交AC于点E，在Rt△BCE中，根据勾股定理可求出BE、CE，进而可将AD的长求出．
解答：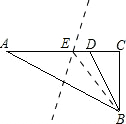
解：作AB的垂直平分线，交AC于点E，
∴AE=BE，∵∠C=90°，∠ABC=75°，∠CBD=30°，∴2∠A=∠BED=30°，
∴tan30°=
=
，
解得：CD=
cm，
∵BC=3 cm，∴BE=6cm，∴CE=3cm，
∴AD=AE+CE-CD=BE+CE-CD=（6+）cm．
点评：本题主要考查直角三角形的性质及勾股定理．
分析：由已知条件可知：BD=2CD，根据勾股定理可求出BD、CD，作AB的垂直平分线，交AC于点E，在Rt△BCE中，根据勾股定理可求出BE、CE，进而可将AD的长求出．
解答：
解：作AB的垂直平分线，交AC于点E，∴AE=BE，∵∠C=90°，∠ABC=75°，∠CBD=30°，∴2∠A=∠BED=30°，
∴tan30°=
=，解得：CD=
cm，∵BC=3 cm，∴BE=6cm，∴CE=3
cm，∴AD=AE+CE-CD=BE+CE-CD=（6+
）cm．点评：本题主要考查直角三角形的性质及勾股定理．
练习册系列答案
相关题目
如图，∠BAC=90°，AD⊥BC，△ABE，△ACF都是等边三角形，则S△ABE：S△ACF等于（ ）| A、AB：AC | B、AD2：DC2 | C、BD2：DC2 | D、AC2：AB2 |
14、如图，∠AOB=90°，∠B=30°，△AOB′可以看作是由△AOB绕点O顺时针旋转α角度得到的，若点A′在AB上，则旋转角α的大小可以是
16、如图，∠C=90°，AD平分∠CAB，DE⊥AB于E，若DB=2DE=6cm，则BC=
已知：如图，∠C=90°，⊙C与AB相交于点D，AC=5，CB=12，求AD．
如图，∠AOB=90°，0C⊥OD，且∠BOC=