题目内容
已知抛物线![]() 的部分图象如图1所示。
的部分图象如图1所示。

(1)求c的取值范围;
(2)若抛物线经过点(0,一1),试确定抛物线![]() 的解析式;
的解析式;
(3)若反比例函数![]() 的图象经过(2)中抛物线上点(1,
的图象经过(2)中抛物线上点(1,![]() ),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较![]() 与
与![]() 的大小。
的大小。
解:(1)根据图象可知c<0,
且抛物线![]() 与
与![]() 轴有两个交点,
轴有两个交点,
所以一元二次方程![]() 有两个不等的实数根。
有两个不等的实数根。
所以,且△=![]() ,
,
所以c<1.
(2)因为抛物线经过点(0.一l),
把![]() 代入
代入![]() .
.
得c= 一1.
故所求抛物线的解析式为![]() .
.
(3)因为反比例函数![]() 的图象经过抛物线
的图象经过抛物线![]() 上的点(1,
上的点(1,![]() ).
).
把![]() 代入
代入![]() ,得
,得![]() .
.
把![]() 代入
代入![]() ,得
,得![]() .
.
所以![]() .
.
画出![]() 的图象如图所示.
的图象如图所示.
观察图象,![]() 与
与![]() 除交点(1,一2)外,还有两个交点大致为(一1,2)和(2,一l).
除交点(1,一2)外,还有两个交点大致为(一1,2)和(2,一l).
把![]() 和
和![]() 分别代入
分别代入![]() 和
和![]() 可知,
可知,
(―1,2)和(2,一l)是![]() 与
与![]() 的两个交点.
的两个交点.
根据图象可知:当![]() 或
或![]() 或
或![]() 时,
时,![]() ;
;
当![]() 或
或![]() 或
或![]() 时,
时,![]() ;
;
当![]() 或
或![]() 时,
时,![]() 时.
时.


练习册系列答案
相关题目
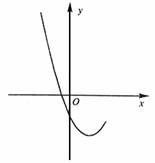

 的部分图象如
的部分图象如  时,x的取值范围.
时,x的取值范围.
 的部分图象如图所示.
的部分图象如图所示.
 的部分图象如
的部分图象如
 时,x的取值范围.
时,x的取值范围.