题目内容
Rt△ABC中,∠ACB=90°,CD为AB上的高,AC=15,BD=16,则△ABC的面积为
- A.120
- B.144
- C.150
- D.216
C
分析:根据已知可判定△ACD∽△ABC,根据相似比可求得AD,AB的长,再利用勾股定理求得BC的长,根据面积公式即可求得其面积.
解答: 解:∵Rt△ABC中,∠ACB=90°,CD为AB上的高
解:∵Rt△ABC中,∠ACB=90°,CD为AB上的高
∴△ACD∽△ABC
∴ =
=
∴AC2=AB•AD
∴225=AD•(AD+16)
∴AD=9
∴AB=25
∴BC=10
∴△ABC的面积为 AC•BC=150
AC•BC=150
故选C.
点评:本题主要考查了直角三角形斜边上的高把三角形分成的两个三角形与原三角形相似.
分析:根据已知可判定△ACD∽△ABC,根据相似比可求得AD,AB的长,再利用勾股定理求得BC的长,根据面积公式即可求得其面积.
解答:
 解:∵Rt△ABC中,∠ACB=90°,CD为AB上的高
解:∵Rt△ABC中,∠ACB=90°,CD为AB上的高∴△ACD∽△ABC
∴
 =
=
∴AC2=AB•AD
∴225=AD•(AD+16)
∴AD=9
∴AB=25
∴BC=10
∴△ABC的面积为
 AC•BC=150
AC•BC=150故选C.
点评:本题主要考查了直角三角形斜边上的高把三角形分成的两个三角形与原三角形相似.

练习册系列答案
相关题目
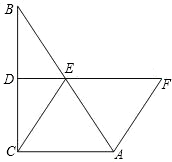 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=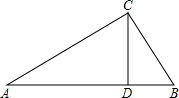 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=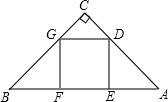 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为