Question

【题目】中，，将线段AB绕点A按逆时针方向旋转得到线段AD，其中连结BD，CD，．

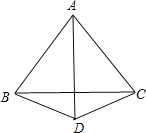
若，，在图1中补全图形，并写出m值．

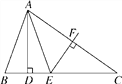
如图2，当为钝角，时，m值是否发生改变？证明你的猜想．

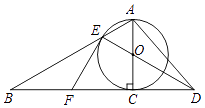
如图3，，，BD与AC相交于点O，求与的面积比．

Answer 1

【答案】（1）m=2（2）m值不发生改变（3）

【解析】

（1）如图1，根据旋转的性质得AB=AD，则AB=AD=AC，于是可判断点B、D、C在以点A为圆心、AB为半径的圆上，则根据圆周角定理可得∠DAC=2∠DBC，即有m=2；
（2）与（1）一样可判断点B、D、C在以点A为圆心、AB为半径的圆上，则根据圆周角定理可得∠DAC=2∠DBC，所以有m=2；
（3）作DH⊥AC于H，如图3，设AB=AC=AD=x，根据等腰直角三角形的性质得∠ABC=45°，利用（2）中的结论和∠DBC+∠DAC=45°可计算出∠DBC=15°，∠CAD=30°，则∠ABD=30°，在△ABO中，根据含30度的直角三角形三边的关系得OB=，，所以OC=AC-A0=，，在Rt△ADH中可计算出DH=，，接着利用三角形面积公式可分别计算出S△OCD＝ ，S△AOB=，然后计算它们的比值．

解：如图，

线段AB绕点A按逆时针方向旋转得到线段AD，

，

而，

，

点B、D、C在以点A为圆心、AB为半径的圆上，

，

即；

值不发生改变理由与一样；

作于H，如图3，

设，

，，

，

，

而，

，解得，

，，

在中，，

，

，

在中，，

，

，

，

：：．