题目内容
四边形ABCD为菱形，对角线AC、BD相交于点O，若AB=5，BD=6，则AC的长为________．
8
分析：由四边形ABCD为菱形，易证得OB=OD=
BD=×6=3，OA=OC，AC⊥BD，然后由勾股定理求得OA的长，继而求得答案．
解答：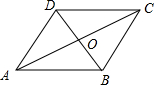
解：∵四边形ABCD是菱形，
∴OB=OD=BD=×6=3，OA=OC，AC⊥BD，
在Rt△AOB中，OA=
=
=4，
∴AC=2OA=8．
故答案为：8．
点评：此题考查了菱形的性质以及勾股定理．此题难度不大，注意掌握数形结合思想的应用．
分析：由四边形ABCD为菱形，易证得OB=OD=
BD=×6=3，OA=OC，AC⊥BD，然后由勾股定理求得OA的长，继而求得答案．解答：
解：∵四边形ABCD是菱形，∴OB=OD=
BD=×6=3，OA=OC，AC⊥BD，在Rt△AOB中，OA=
==4，∴AC=2OA=8．
故答案为：8．
点评：此题考查了菱形的性质以及勾股定理．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
意一点，过点P作PC⊥x轴于点C，PO⊥y轴于点D．
如图，四边形ABCD为菱形，则tan| A |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
点N，过点N作NP⊥BD，交BD于点P，连接MP，当动点M运动了t秒时．
如图，每个小方格都是边长为1个单位的小正方形，B，C，D三点都是格点（每个小方格的顶点叫格点）．