题目内容
 如图,每个小方格都是边长为1个单位的小正方形,B,C,D三点都是格点(每个小方格的顶点叫格点).
如图,每个小方格都是边长为1个单位的小正方形,B,C,D三点都是格点(每个小方格的顶点叫格点).(1)找出格点A,连接AB,AD使四边形ABCD为菱形;
(2)画出菱形ABCD沿直线l翻折后的图形;
(3)请求出四边形ABCD的面积.
分析:(1)根据菱形的性质以及网格结构找出点A的位置,然后连接即可;
(2)根据网格结构找出点A、B、C、D关于直线l的对称点的位置,然后顺次连接即可;
(4)根据勾股定理列式求出AC、BD的长,然后根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.
(2)根据网格结构找出点A、B、C、D关于直线l的对称点的位置,然后顺次连接即可;
(4)根据勾股定理列式求出AC、BD的长,然后根据菱形的面积等于对角线乘积的一半列式进行计算即可得解.
解答: 解:(1)如图所示,四边形ABCD为菱形;
解:(1)如图所示,四边形ABCD为菱形;
(2)如图所示,菱形AB′C′D′即为所求作的菱形ABCD沿直线l翻折后的图形;
(3)根据勾股定理,AC=
=2
,
BD=
=4
,
所以,S四边形ABCD=
AC•BD=
×2
×4
=8.
 解:(1)如图所示,四边形ABCD为菱形;
解:(1)如图所示,四边形ABCD为菱形;(2)如图所示,菱形AB′C′D′即为所求作的菱形ABCD沿直线l翻折后的图形;
(3)根据勾股定理,AC=
| 22+22 |
| 2 |
BD=
| 42+42 |
| 2 |
所以,S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查了利用轴对称变换作图,熟练掌握网格结构与菱形的性质,找出对应点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 24、如图,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
24、如图,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.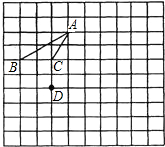 ,得到对应△A′B′C′.
,得到对应△A′B′C′. 如图,每个小方格都是边长为1的正方形,
如图,每个小方格都是边长为1的正方形, 如图,每个小方格都是边长为1个单位长度的小正方形.
如图,每个小方格都是边长为1个单位长度的小正方形.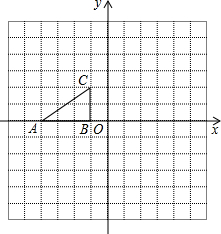 如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.
如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.