Question

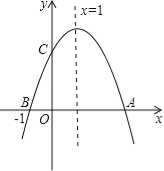
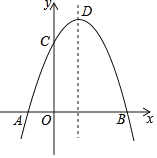
【题目】如图，抛物线y＝﹣x2+2x+m交x轴于点A（a，0）和B（b，0），交y轴于点C，抛物线的顶点为D，下列四个结论：

①点C的坐标为（0，m）；

②当m＝0时，△ABD是等腰直角三角形；

③若a＝﹣1，则b＝4；

④抛物线上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2．

其中结论正确的序号是_____．

Answer 1

【答案】①②④

【解析】

①抛物线与y轴的交点坐标即为C点坐标，横坐标为0，当x=0时求出y值即为C点纵坐标，y=﹣x2+2x+m=m，可求出C点坐标.

②当m＝0时，抛物线已知，可求出抛物线与x轴两个交点坐标，确定对称轴，即可确定△ABD是否是等腰直角三角形.

③若a＝﹣1，即知道抛物线与x轴一个交点坐标，再根据可确定的对称轴，即可推出抛物线与x轴另外一个交点坐标，得出b值.

④根据x1＜1＜x2，且x1+x2＞2，可以得出点Q到直线x=1的距离比点P到直线x=1的距离大，所以y1＞y2.

①抛物线与y轴的交点坐标为C（0，y），

当x=0时，y=﹣x2+2x+m=m

故C（0，y）

所以①正确

②当m＝0时，抛物线与x轴的两个交点坐标分别为（0，0）、（2，0）

对称轴为x＝1，顶点坐标(1，1)

∴△ABD是等腰直角三角形

故②正确

③当a＝﹣1时，抛物线与x轴的一个交点坐标为（﹣1，0）

∵对称轴x＝1

∴另一个交点坐标为（3，0）

∴b＝3

故③错误

④因为x1＜1＜x2，且x1+x2＞2，则点Q到直线x=1的距离比点P到直线x=1的距离大，所以y1＞y2

故④正确．

故答案为：①②④．