Question

将一块长18米，宽15米的矩形荒地修建成一个花园，所占的面积为原来荒地面积的三分之二． （精确到0.1米）
（1）设计方案1（如图①）花园中修两条互相垂直且宽度相等的小路；
（2）设计方案2（如图②）花园中每个角的扇形都相同．

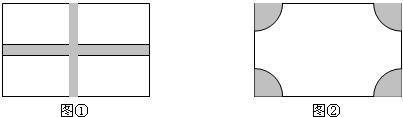
以上两种方案是否都能符合条件？若能，请计算出图①中小路的宽和图②中扇形的半径；若不能符合条件，请说明理由．

Answer 1

分析：（1）设出小路的宽度为x米，表示出两条小路的面积，而小路的面积为原来荒地面积的三分之一，列出方程解答即可；
（2）设出扇形的半径为y米，则四个扇形的面积和恰好等于一个圆的面积，而四个扇形的面积和为原来荒地面积的三分之一，列出方程解答即可．

解答：解：（1）设小路的宽度为x米，根据题意列方程得，
18x+15x-x²=18×15×

1

3

，
解得x₁=3，x₂=30（不合题意，舍去）；
答：图①中小路的宽为3米．
（2）设扇形的半径为y米，根据题意列方程得，
πy²=18×15×

1

3

，
解得y₁≈5.4，y₂≈-5.4（不合题意，舍去）；
答：扇形的半径约为5.4米．

点评：此题主要考查长方形和扇形面积的计算方法，解答时注意题目中蕴含的数量关系．