题目内容
5.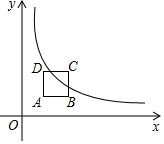 在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图,双曲线y=$\frac{3}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{3}$-1≤a$≤\sqrt{3}$.
在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图,双曲线y=$\frac{3}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{3}$-1≤a$≤\sqrt{3}$.
分析 根据题意得出C点的坐标(a+1,a+1),然后分别把A、C的坐标代入求得a的值,即可求得a的取值范围.
解答 解:∵A点的坐标为(a,a).
根据题意C(a+1,a+1),
当C在曲线y=$\frac{3}{x}$(x>0)时,则a+1=$\frac{3}{a+1}$,
解得a=$\sqrt{3}$-1,
当A在曲线y=$\frac{3}{x}$(x>0)时,则a=$\frac{3}{a}$,
解得a=$\sqrt{3}$,
∴a的取值范围是$\sqrt{3}$-1≤a$≤\sqrt{3}$.
故答案为$\sqrt{3}$-1≤a$≤\sqrt{3}$.
点评 本题考查了反比例函数图象上点的坐标特征,点的坐标适合解析式是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
15.下列以a,b,c为三边的三角形中,是直角三角形的是( )
| A. | $a=\sqrt{3}$,$b=\sqrt{4}$,$c=\sqrt{5}$ | B. | a=1,b=2,$c=2\sqrt{5}$ | C. | a=2,b=3,$c=\sqrt{5}$ | D. | a=1,$b=2\sqrt{2}$,c=2 |
16.10g盐溶入100g水中,盐占盐水的( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{11}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{2}$ |
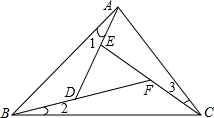 如图,∠1=∠2=∠3,且∠BAC=70°,∠DFE=50°,则∠ABC的度数为60°.
如图,∠1=∠2=∠3,且∠BAC=70°,∠DFE=50°,则∠ABC的度数为60°.