题目内容
 问题背景:已知x是实数,求y=
问题背景:已知x是实数,求y=| x2+4 |
| (12-x)2+9 |
| x2+22 |
| (12-x)2+32 |
| x2+22 |
| (12-x)2+32 |
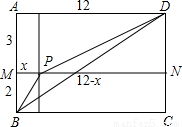
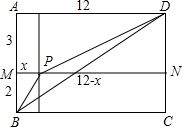
解:构造矩形ABCD,使AB=5,AD=12.在AB上截取AM=3,做矩形AMND.设点P是MN上一点MP=x,则PN=12-x,
|
(1)我们把上述求最值问题的方法叫做构图法.请仿造上述方法求y=
| 1+x2 |
| 25+(8-x)2 |
探索创新:
(2)已知a,b,c,d是正实数且a+b+c+d=1,试运用构图法求
| a2+b2 |
| b2+c2 |
| c2+d2 |
| d2+a2 |
分析:(1)根据勾股定理,
和
表示矩形的对角线长,即可构造矩形ABCD,使AB=6,AD=8.在AB上截取AM=5,作矩形AMND.设点P是MN上一点MP=x,则PN=8-x,利用两点之间线段最短即可证得;
(2)根据已知可以构造一个边长分别是a+b+c+d的正方形,即可利用两点之间线段最短即可求解.
| 1+x2 |
| 25+(8-x)2 |
(2)根据已知可以构造一个边长分别是a+b+c+d的正方形,即可利用两点之间线段最短即可求解.
解答: 解:(1)构造矩形ABCD,使AB=6,AD=8.
解:(1)构造矩形ABCD,使AB=6,AD=8.
在AB上截取AM=5,作矩形AMND.
设点P是MN上一点MP=x,则PN=8-x,
PB=
,
PD=
BD=
=10
∵PB+PD≥BD=10
∴y的最小值是10;
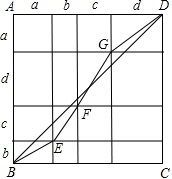
(2)构造图形,使BE=
,EF=
,FG=
,DG=
,
则BE+EF+FG+DG=
+
+
+
的最小值等于BD=
=
=
=
.
 解:(1)构造矩形ABCD,使AB=6,AD=8.
解:(1)构造矩形ABCD,使AB=6,AD=8.在AB上截取AM=5,作矩形AMND.
设点P是MN上一点MP=x,则PN=8-x,
PB=
| x2+12 |
PD=
| (8-x)2+52 |
BD=
| 62+82 |
∵PB+PD≥BD=10
∴y的最小值是10;
(2)构造图形,使BE=
| a2+b2 |
| b2+c2 |
| c2+d2 |
| d2+a2 |
则BE+EF+FG+DG=
| a2+b2 |
| b2+c2 |
| c2+d2 |
| d2+a2 |
| BC2+CD2 |
| (a+b+c+d)2+(a+b+c+d)2 |
| 12+12 |
| 2 |

点评:本题考查了两点之间线段最短,正确理解题意是关键.

练习册系列答案
相关题目
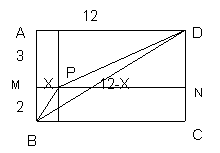 解:构造矩形ABCD,使AB=5,AD=12.在AB上截取AM=3,做矩形AMND。设点P是MN上一点MP=x,则PN=12-x,
解:构造矩形ABCD,使AB=5,AD=12.在AB上截取AM=3,做矩形AMND。设点P是MN上一点MP=x,则PN=12-x,
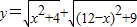 的最小值.要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于
的最小值.要解决这个问题需现判断出0<x<12,继而联想到构造以边长为2+3和12为边的矩形,找出等于 的线段,再比较
的线段,再比较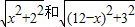 和矩形对角线的大小.
和矩形对角线的大小.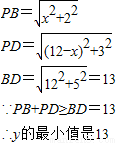
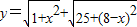 的最小值.
的最小值.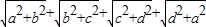 的最小值.
的最小值.