题目内容
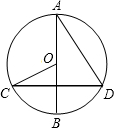
如图，⊙O上三点A、B、C把圆分成
、
和
，三段弧的度数之比为3：1：2，连接AB、BC、CA，求证：△ABC是直角三角形．
 |
| AB |
|
| BC |
|
| AC |
证明：∵
、
、
三段弧的度数之比为3：1：2．
∴
的度数为：
×360°=180°
∴
的度数为：
×360°=60°，
∴
的度数为：
×360°=120°，
∴∠C=90°，∠A=30°，∠B=60°
∴△ABC是直角三角形
|
| AB |
|
| BC |
|
| AC |
∴
|
| AB |
| 3 |
| 3+1+2 |
∴
|
| BC |
| 1 |
| 3+1+2 |
∴
|
| AC |
| 2 |
| 3+1+2 |
∴∠C=90°，∠A=30°，∠B=60°
∴△ABC是直角三角形
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
