Question

【题目】（问题情境）

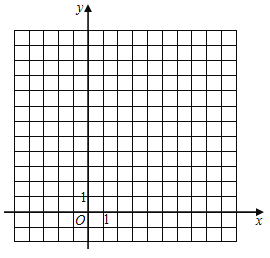
我们知道若一个矩形是的周长固定，当相邻两边相等，即为正方形时，它的面积最大．反过来，若一个矩形的面积固定，它的周长是否会有最值呢？

（探究方法）

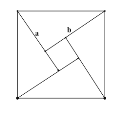
用两个直角边分别为，的4个全等的直角三角形可以拼成一个正方形。若，可以拼成如图所示的正方形，从而得到，即；当时，中间小正方形收缩为1个点，此时正方形的面积等于4个直角三角形面积的和.即．于是我们可以得到结论：，为正数，总有，当且仅当时，代数式取得最小值．另外，我们也可以通过代数式运算得到类似上面的结论：

∵，∴，

∴对于任意实数，总有，且当时，代数式取最小值．

使得上面的方法，对于正数，，试比较和的大小关系．

（类比应用）

利用上面所得到的结论完成填空

（1）当时，代数式有最 值为 ．

（2）当时，代数式有最 值为 ．

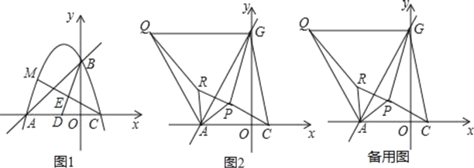
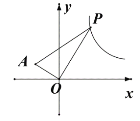
（3）如图，已知是反比例函数图象上任意一动点，，，试求的最小面积．

Answer 1

【答案】（1）小；4 （2）小； （3）1

【解析】

探究方法：仿照给定的方法，即可得出这一结论；

（1）直接利用求解；

（2）变形解答即可；

（3）设，写出面积表达式，利用上面的结论做答即可．

解：探究：∵，

∴成立；

（1）由可以得到：，

∴当时，代数式有最小值为4．

（2）构造已知条件形式：，

∴当时，代数式有最小值为．

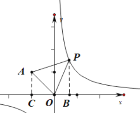
（3）过P做PB⊥x轴于点B，过A作AC⊥x轴于点C，设，由题意得：

=

=

=

=

∴的最小面积为1．