题目内容
下面是2014年1月的日历表,请你根据它研究以下问题:

(1)任意框出日历中偶9个数组成的方框,请分析这9个数之和与这个方框正中间的数有什么关系?
(2)这个关系式对其他这样的方框成立吗?你能用代数式表示这个关系式吗?
(3)这个关系式对任何一个月的日历都成立吗?为什么?
(4)如果将方框改为十字形框,你能发现哪些规律?

(1)任意框出日历中偶9个数组成的方框,请分析这9个数之和与这个方框正中间的数有什么关系?
(2)这个关系式对其他这样的方框成立吗?你能用代数式表示这个关系式吗?
(3)这个关系式对任何一个月的日历都成立吗?为什么?
(4)如果将方框改为十字形框,你能发现哪些规律?
考点:一元一次方程的应用
专题:
分析:(1)设中间的数为x,表示出其余的数,看相加的结果与中间的数的关系即可;
(2)根据中间数与上下、左右数的关系分析解答;
(3)根据以上规律可得这个关系对任何一个月的月历都成立;
(4)规律:十字形框中5个数之和等于正中间数的5倍.
(2)根据中间数与上下、左右数的关系分析解答;
(3)根据以上规律可得这个关系对任何一个月的月历都成立;
(4)规律:十字形框中5个数之和等于正中间数的5倍.
解答:解:(1)设正中心的数为x,则,
方框中的9个数之和为:
(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x.
所以这9个数之和是方框正中间的数的9倍.
(2)结合图表正中间那个日期为x,相邻两数减1与加1,正中间这一行上下分别加7与减7,
据此得到相同的结果,所以这个关系对其他方框成立,用代数式表示即是:中间数为x,则9个数之和为9x.
(3)这个关系对任何一个月的月历都成立,因为无论哪个月都有正中间那个日期为x,相邻两数减1与加1,正中间这一行上下分别加7与减7.
(4)将方框改为十字形框,规律:十字形框中5个数之和等于正中间数的5倍.
方框中的9个数之和为:
(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x.
所以这9个数之和是方框正中间的数的9倍.
(2)结合图表正中间那个日期为x,相邻两数减1与加1,正中间这一行上下分别加7与减7,
据此得到相同的结果,所以这个关系对其他方框成立,用代数式表示即是:中间数为x,则9个数之和为9x.
(3)这个关系对任何一个月的月历都成立,因为无论哪个月都有正中间那个日期为x,相邻两数减1与加1,正中间这一行上下分别加7与减7.
(4)将方框改为十字形框,规律:十字形框中5个数之和等于正中间数的5倍.
点评:此题考查的是一元一次方程的应用和列代数式,解决本题的难点是发现日历中左右相邻的数相隔1,上下相邻的数相隔7.

练习册系列答案
相关题目
 如图,是由棱长为1的正方体搭成的积木的三视图,则图中棱长为1的正方体的个数是( )
如图,是由棱长为1的正方体搭成的积木的三视图,则图中棱长为1的正方体的个数是( )| A、4个 | B、5个 | C、6个 | D、7个 |
用科学记数法表示860 000的结果是( )
| A、86×104 |
| B、8.6×105 |
| C、0.86×106 |
| D、8.6×106 |
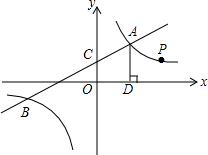 如图,一次函数y1=k1x+2与反比例函数y2=
如图,一次函数y1=k1x+2与反比例函数y2= 如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上两树间的坡面距离(结果保留小数点后一位).
如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上两树间的坡面距离(结果保留小数点后一位).