题目内容
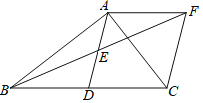
【题目】如图,在菱形ABCD中,![]() ,∠DAB=60°,点E是AD边的中点
,∠DAB=60°,点E是AD边的中点![]() 点M是AB边上一动点
点M是AB边上一动点![]() 不与点A重合
不与点A重合![]() ,延长ME交射线CD于点N,连接MD、AN.
,延长ME交射线CD于点N,连接MD、AN.
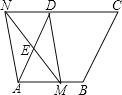
![]() 求证:四边形AMDN是平行四边形;
求证:四边形AMDN是平行四边形;
![]() 当AM的值为______时,四边形AMDN是菱形
当AM的值为______时,四边形AMDN是菱形![]() 并说明理由.
并说明理由.
【答案】(1)详见解析;(2)2
【解析】
(1)利用菱形的性质和已知条件可证明四边形AMDN的对边平行且相等即可;
(2)当平行四边形AMND的邻边AM=DM时,四边形为菱形,利用已知条件再证明三角形AMD是等边三角形即可.
(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)当AM的值为2时,四边形AMDN是菱形.理由如下:
∵AM=2,
∴AM=AD=2,
∴△AMD是等边三角形,
∴AM=DM,
∴平行四边形AMDN是菱形,
故答案为:2.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
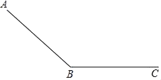
A.270B.280C.375D.450