题目内容
16.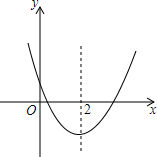 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②a-b+c<0;③4a+2b+c>0;④b2-4ac>0.其中正确的结论①④(填序号).
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②a-b+c<0;③4a+2b+c>0;④b2-4ac>0.其中正确的结论①④(填序号).
分析 ①首先根据抛物线开口向上,可得a>0;然后根据抛物线的对称轴为直线x=-$\frac{b}{2a}$>0,可得b<0;最后根据抛物线与y轴的交点在x轴上方,可得c>0,所以abc<0,据此判断即可.
②根据二次函数y=ax2+bx+c(a≠0)的图象,可得当x=-1时,y>0,所以a-b+c>0,据此判断即可.
③根据二次函数y=ax2+bx+c(a≠0)的图象,可得当x=2时,y<0,所以4a+2b+c<0,据此判断即可.
④根据抛物线与x轴有2个交点,可得△=b2-4ac>0,据此判断即可.
解答 解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$>0,
∴b<0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,
∴结论①正确.
∵当x=-1时,y>0,
∴a-b+c>0,
∴结论②错误.
∵x=2时,y<0,
∴4a+2b+c<0,
∴结论③错误;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,
∴结论④正确.
综上,可得正确的结论有:①④.
故答案为:①④.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
相关题目
6. 如图,在⊙O中,∠BOC=80°,则∠A的度数为( )
如图,在⊙O中,∠BOC=80°,则∠A的度数为( )
 如图,在⊙O中,∠BOC=80°,则∠A的度数为( )
如图,在⊙O中,∠BOC=80°,则∠A的度数为( )| A. | 80° | B. | 20° | C. | 30° | D. | 40° |
11.下列各方程,变形不正确的是( )
| A. | $\frac{x-3}{5}-\frac{x+4}{2}=1$去分母化为2(x-3)-5(x+4)=10 | |
| B. | 2(x-3)-5(x+4)=10去括号为:2x-3-5x+20=10 | |
| C. | 2x-3-5x+20=10移项得:2x-5x=10-20+3 | |
| D. | 2x-5x=10-20+3合并同类项得:-3x=-7 |
1.将二次函数y=x2的图象向下平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
8.玉树地震后,青海省某乡镇中学的同学用下面的方法检测教室的房梁是否水平:如图,在等腰直角三角尺斜边中点栓一条细绳,细绳的另一端挂一个铅锤,把这块三角尺的斜边贴在房梁上,结果绳子经过三角尺的直角顶点,于是同学们确信房梁是水平的,其理由是( )
| A. | 等腰三角形两腰等分 | |
| B. | 等腰三角形两底角相等 | |
| C. | 三角形具有稳定性 | |
| D. | 等腰三角形的底边中线和底边上的高重合 |
6.方程x2-2(3x-2)=5的一般形式是( )
| A. | x2-6x+4=5 | B. | x2-6x-4=5 | C. | x2-6x-1=0 | D. | x2-6x-9=0 |
 如图,△ABC中,∠ABC与∠ACB的角平分线交于点F,过点F作DE∥BC,交AB于D,交AC于点E.求证:DE=DB+EC.
如图,△ABC中,∠ABC与∠ACB的角平分线交于点F,过点F作DE∥BC,交AB于D,交AC于点E.求证:DE=DB+EC.