题目内容
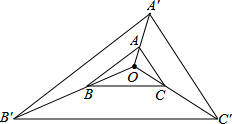如图，以O为位似中心画△ABC得到位似图形△A′B′C′且OA：AA′=1：2，则
=
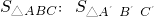- A.1：2
- B.1：4
- C.1：3
- D.1：9
D
分析：△ABC与△A′B′C′是位似图形，由OA：AA′=1：2可得两个图形的位似比，面积的比等于位似比的平方．
解答：由△ABC与△A′B′C′是位似图形且由OA：AA′=1：2．
可得两位似图形的位似比为：1：3，所以两位似图形的面积比为：1：9，
故选：D．
点评：本题考查了位似图形的性质：面积的比等于位似比的平方．
分析：△ABC与△A′B′C′是位似图形，由OA：AA′=1：2可得两个图形的位似比，面积的比等于位似比的平方．
解答：由△ABC与△A′B′C′是位似图形且由OA：AA′=1：2．
可得两位似图形的位似比为：1：3，所以两位似图形的面积比为：1：9，
故选：D．
点评：本题考查了位似图形的性质：面积的比等于位似比的平方．
练习册系列答案
相关题目
8、如图，以A为位似中心，将△ADE放大2倍后，得位似图形△ABC，若s1表示△ADE的面积，s2表示四边形DBCE的面积，则s1：s2=（ ）
17、如图，以O为位似中心，把五边形ABCDE的面积扩大为原来的4倍，得五边形A1B1C1D1E1，则OD：OD1=
如图，以O为位似中心，将五边形ABCDE放大得到五边形A′B′C′D′E′，已知OA=10cm，OA′=30cm，若S五边形A′B′C′D′E′=27cm2，则S五边形ABCDE=
，则OD∶
= 
表示△ADE的面积，
表示四边形DBCE的面积，则
= （ ）