题目内容
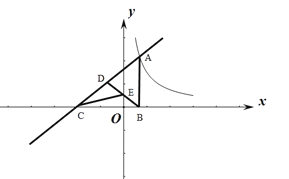
【题目】已知直线y=2x+b与反比例函数y=![]() 的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
的(k>0)图象交于点A,过点A作AB⊥x轴于点B,点D为线段AC的中点,BD交y轴于点E.
(1)若k=8,且点A的横坐标为1,求b的值;
(2)已知△BEC的面积为4,则k的值为多少?
(3)在(2)的条件下,已知点E为△ABC的重心,且OE=2,求直线AC的解析式.
【答案】(1)b=6;(2)k=8;(3)![]()
【解析】
(1)将点![]() 的横坐标
的横坐标![]() 代入解析式,即可求得
代入解析式,即可求得![]() 点坐标为(1,8),再代入一次函数解析式即可求得
点坐标为(1,8),再代入一次函数解析式即可求得![]() ;
;
(2)过点![]() 作
作![]() 轴与点
轴与点![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,易证
,易证![]() ,再分别设出每个点的坐标,即可表示出
,再分别设出每个点的坐标,即可表示出![]() ,因为点A既在抛物线上也在直线上,通过坐标进行转化化简后,可以求得
,因为点A既在抛物线上也在直线上,通过坐标进行转化化简后,可以求得![]() ;
;
(3)△BEC的面积为4,利用重心的性质:可知DE:BE=1:2,进而可以求得△ABC的面积为12,进而求得BC、AB,过点D作DH![]() AB于H,交
AB于H,交![]() 轴于K,通过平行线分线段成比例,分别可求得DK、KH,即可知A点坐标,代入一次函数解析式,即可求解.
轴于K,通过平行线分线段成比例,分别可求得DK、KH,即可知A点坐标,代入一次函数解析式,即可求解.
解:(1)∵![]() ,则反比例函数解析式为
,则反比例函数解析式为![]() ,将点A的横坐标
,将点A的横坐标![]() 代入解析式,
代入解析式,
解得![]() ,故
,故![]() 点坐标为(1,8),再将点A代入一次函数解析式得
点坐标为(1,8),再将点A代入一次函数解析式得![]() ,
,
解得![]() =6;
=6;
(2)过点![]() 作
作![]() 轴与点
轴与点![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,则有
,则有![]() ,
,
∴![]() ,
,
∵![]() 为直角三角形,且点
为直角三角形,且点![]() 为中点,
为中点,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中 ,
,
∴![]() ,
,
∴![]() ,
,
设点B的坐标为(![]() ,
,![]() ),则A点的坐标为(
),则A点的坐标为(![]() ,
,![]() ),C点的坐标为(
),C点的坐标为(![]() ,
,![]() ),
),
G点坐标为(![]() ,
,![]() ),F点坐标为(
),F点坐标为(![]() ,
,![]() ),
),
∴ ![]() ,
,
而点A也在一次函数图像上,故![]() ,代入上式,整理得:
,代入上式,整理得:
![]() ,即
,即![]() ,而
,而![]() ,
,
故![]() ,即
,即![]() ;
;
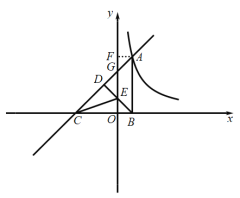
(3)∵E为重心,根据重心的性质,
∴DE:BE=1:2,而![]() ,
,
∴![]() ,即
,即![]() ,
,
∵D为AC中点,
∴![]() ,
,
∵![]() ,OE=
,OE=![]() ,
,
∴BC=![]() ,
,
∴![]() , 即AB=
, 即AB=![]() ,
,
过点D作DH![]() AB于点H,交
AB于点H,交![]() 轴于点
轴于点![]() ,
,

则有:![]() ,DH为中位线,
,DH为中位线,
∴![]() , 即
, 即![]() ,
,
求得:![]() ,
,![]() ,
,
即点A坐标为(![]() ,6),再代入
,6),再代入![]() 中,解得:
中,解得:![]() .
.
故直线AC的解析式为:![]() .
.