题目内容
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在 .
【答案】分析:由图可知∠BPD一定是钝角,若要△ABC∽△PBD,则PB、PD与AB、AC的比值必须相等,可据此进行判断.
解答:解:由图知:∠BPD一定是钝角;
∵△ABC∽△PBD,则∠BPD=∠BAC;
∵BA:AC=1: ,
,
∴BP:PD=1: 或BP:PD=
或BP:PD= :1;
:1;
只有P3点符合这样的要求,故P点应该在P3处.
点评:此题主要考查的是相似三角形的判定:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
解答:解:由图知:∠BPD一定是钝角;
∵△ABC∽△PBD,则∠BPD=∠BAC;
∵BA:AC=1:
 ,
,∴BP:PD=1:
 或BP:PD=
或BP:PD= :1;
:1;只有P3点符合这样的要求,故P点应该在P3处.
点评:此题主要考查的是相似三角形的判定:如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
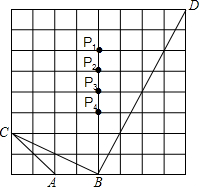 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
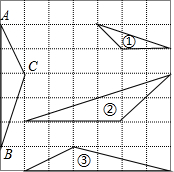 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF. 作图计算题.
作图计算题.