题目内容
19.若等腰三角形两边为4,10,则底角的正弦值是$\frac{2\sqrt{6}}{5}$.分析 根据三角形三边关系定理确定腰和底边的长.作底边上的高,利用三角函数的定义求解.
解答 解:∵4+4=8<10,
∴AB=AC=10,BC=4.
过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BD=DC=$\frac{1}{2}$BC=2.
∵AB=AC=10,
∴AD=$\sqrt{1{0}^{2}-{2}^{2}}$=$\sqrt{96}$=4$\sqrt{6}$,
∴sin∠ABD=$\frac{AD}{AB}$=$\frac{4\sqrt{6}}{10}$=$\frac{2\sqrt{6}}{5}$,
故答案为$\frac{2\sqrt{6}}{5}$.
点评 本题考查了三角函数的定义以及三角形三边关系定理,掌握分类思想是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若3x+2y=0,则代数式$\frac{2x+3y}{2x-3y}$的值为( )
| A. | 1 | B. | -1 | C. | -$\frac{5}{13}$ | D. | 不能确定 |
 请你画出如图几何体的三视图.
请你画出如图几何体的三视图.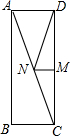 如图,在矩形ABCD中,AD=3,AB=9,M是DC上一点,DM=4,N是AC上的一个动点,则△DMN的周长的最小值是$\sqrt{34}$+4.
如图,在矩形ABCD中,AD=3,AB=9,M是DC上一点,DM=4,N是AC上的一个动点,则△DMN的周长的最小值是$\sqrt{34}$+4.