题目内容
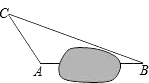 在一次综合实践活动中,同学们要测量某公园的人工湖两侧A、B两个凉亭之间的距离(如图)现测得AC=30m,BC=70m,∠CAB=120°,则A、B两个凉亭之间的距离为
在一次综合实践活动中,同学们要测量某公园的人工湖两侧A、B两个凉亭之间的距离(如图)现测得AC=30m,BC=70m,∠CAB=120°,则A、B两个凉亭之间的距离为分析:过C作AB的垂线CD,在构建的两个直角三角形中,通过解直角三角形分别求出BD、AD的长,进而可根据AB=BD-AD求出AB的距离.
解答: 解:如图,过C作CD⊥AB于D交BA的延长线于D.
解:如图,过C作CD⊥AB于D交BA的延长线于D.
Rt△ACD中,∠CAD=180°-∠CAB=60°,AC=30,
CD=AC•sin60°=30×
=15
.
AD=
AC=15.
Rt△BCD中,BC=70m,CD=15
m,
由勾股定理得:BD=
=
=65.
∴AB=BD-AD=50(m).
即A、B两个凉亭间的距离为50m.
 解:如图,过C作CD⊥AB于D交BA的延长线于D.
解:如图,过C作CD⊥AB于D交BA的延长线于D.Rt△ACD中,∠CAD=180°-∠CAB=60°,AC=30,
CD=AC•sin60°=30×
| ||
| 2 |
| 3 |
AD=
| 1 |
| 2 |
Rt△BCD中,BC=70m,CD=15
| 3 |
由勾股定理得:BD=
| BC2-CD2 |
702-(15
|
∴AB=BD-AD=50(m).
即A、B两个凉亭间的距离为50m.
点评:此题主要考查的是解直角三角形的应用;
在已知直角三角形边和角的情况下,通常应用锐角三角函数解直角三角形;
在已知直角三角形边的情况下,通常用勾股定理和射影定理求解.
在已知直角三角形边和角的情况下,通常应用锐角三角函数解直角三角形;
在已知直角三角形边的情况下,通常用勾股定理和射影定理求解.

练习册系列答案
相关题目


 (2013•贵阳)在一次综合实践活动中,小明要测某地一座古塔AE的高度,如图,已知塔基AB的高为4m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5m到达D点,又测得塔顶E的仰角为50°.(人的身高忽略不计)
(2013•贵阳)在一次综合实践活动中,小明要测某地一座古塔AE的高度,如图,已知塔基AB的高为4m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5m到达D点,又测得塔顶E的仰角为50°.(人的身高忽略不计)