题目内容
(本题满分10分)抛物线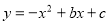 与x轴交与
与x轴交与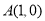 ,
,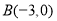 两点,
两点,
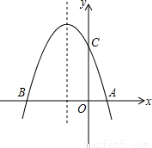
(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(1)y=-x2-2x+3;(2)存在Q(-1,2).
【解析】
试题分析:(1)把A(1,0)B(-3,0)代入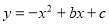 然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
试题解析:解(1)把A(1,0)B(-3,0)代入到
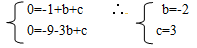 3分
3分
∴抛物线的解析式为y=-x2-2x+3 5分
(2)存在。 6分
过B、C作直线BC与对称轴x=-1的交点就是Q点,
设直线BC解析式为y=kx+b,把B(-3,0)C(0,3)代入到
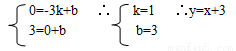
令XQ=-1 得YQ=2 ∴Q(-1,2) 10分
考点:1.待定系数法求函数解析式;2. 轴对称的性质.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
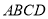 的边长为4,将其沿
的边长为4,将其沿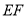 折叠,则图中①②③④四个三角形的周长之和为 .
折叠,则图中①②③④四个三角形的周长之和为 .
 -4ax+4a=_________.
-4ax+4a=_________. ,其中
,其中 .
. 为锐角
为锐角 的外接圆,已知
的外接圆,已知 ,那么
,那么 的度数为 °.
的度数为 °.
