题目内容
(本题满分10分)如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

25+5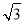 km
km
【解析】
试题分析:过点A作AB的垂线交DC延长线于点E,过点E作l1的垂线与l1、l2分别交于点H,F,则HF⊥l2.根据条件可证四边形ABCE是矩形,从而DE=DC+CE=DC+AB=50.在Rt△DEF中,根据三角函数求得EF,在Rt△AEH中,根据三角函数求得EH,再根据HF=EF+HE即可求解.
试题解析:如图,过点A作AB的垂线交DC延长线于点E,过点E作l1的垂线与l1、l2分别交于点H,F,则HF⊥l2.

由题意知AB⊥BC,BC⊥CD,又AE⊥AB,
∴四边形ABCE是矩形.∴AE=BC,AB=EC.
∴DE=DC+CE=DC+AB=50.
又AB与l1成30°角,∴∠EDF=30°,∠EAH=60°.
在Rt△DEF中,EF=DEsin30°=50×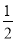 =25.
=25.
在Rt△AEH中,EH=AEsin60°=10×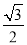 =5
=5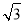 ,
,
所以HF=EF+HE=25+5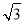 km.
km.
考点:解直角三角形的应用.
考点分析: 考点1:函数基础知识 函数的定义:一般地,在一个变化过程中,如果有两个自变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
对函数概念的理解,主要抓住以下三点:
①有两个变量;
②一个变量的每一个数值随着另一个变量的数值的变化而变化;
③对于自变量每一个确定的值,函数有且只有一个值与之对应。
例如:y=±x,当x=1时,y有两个对应值,所以y=±x不是函数关系。对于不同的自变量x的取值,y的值可以相同,例如,函数:y=|x|,当x=±1时,y的对应值都是1。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 -9x = .
-9x = .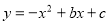 与x轴交与
与x轴交与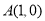 ,
,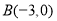 两点,
两点,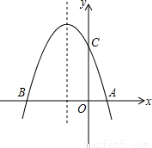
 、
、 ,规定
,规定 ,若
,若 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 与
与 互为倒数,则
互为倒数,则 等于( )
等于( ) B.
B. C.
C. D.
D.


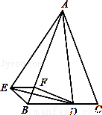
 _______.
_______.
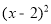 +1 B.y=
+1 B.y=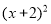 +1
+1