Question

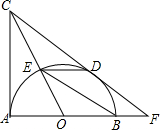
8．AB为圆O的直径，点C在半圆上从点A运动到点B（点C不与A，B重合），过点B作圆O的切线，交AC的平行线OD于点D，连结CB交OD于E．
（1）求证：无论点O在何处，CD总是圆O的切线；
（2）若记AC=x，OD=y，请列出y与x的函数关系式，并写出自变量的取值范围．
（3）试探索：当点C运动到何处时，四边形CAOD是平行四边形，请说明理由，并求出此时点E运动的弧长．

Answer 1

分析 （1）连接OC，由AB为圆O的直径，得到∠ACB=90°，由于AC∥OD，求出∠OEB=90°，于是得到OD垂直平分BC，得到BD=CD，证出∠DBC=∠DCB，根据等腰三角形的性质得到∠OCB=∠OBC，根据等量代换得到∠OCD=90°，于是得到结论；
（2）设圆O的半径为r，由于AC∥OD，得到∠OAC=∠DOB，通过△ABC∽△OBD，列比例式即可得到结果；
（3）当点C运动到弧AB的中点时，四边形CAOD是平行四边形，若C是弧AB的中点，连接OC，则∠AOC=∠BOC=90°，根据CD是⊙O的切线，得到∠ODC=90°，于是得到AO∥CD，由于AC∥OD，根据平行四边形的判定和定理得到四边形CAOD是平行四边形，由于点E是BC的中点，于是得到当点C运动到弧AB的中点，点E运动的弧长=$\frac{90π•\frac{1}{2}r}{180}$=$\frac{1}{4}π$r．

解答 （1）证明：连接OC，∵AB为圆O的直径，
∴∠ACB=90°，
∵AC∥OD，
∴∠OEB=90°，
∴OD垂直平分BC，
∴BD=CD，
∴∠DBC=∠DCB，
∵OC=OB，∴∠OCB=∠OBC，
∵BD切⊙O于B，
∴∠DBC+∠OBC=90°，
∴∠OCB+∠BCD=90°，
∴∠OCD=90°，
∴CD是⊙O的切线；

（2）设圆O的半径为r，∵AC∥OD，
∠OAC=∠DOB，
由（1）知，∠ACB=∠BCD=90°，
∴△ABC∽△OBD，
∴$\frac{OB}{AC}=\frac{OD}{AB}$，即$\frac{r}{x}=\frac{y}{2r}$，
∴y=$\frac{2{r}^{2}}{x}$ （0＜x＜2r），

（3）当点C运动到弧AB的中点时，四边形CAOD是平行四边形，
若C是弧AB的中点，连接OC，则∠AOC=∠BOC=90°，
∵CD是⊙O的切线，∴∠ODC=90°，
∴AO∥CD，∵AC∥OD，
∴四边形CAOD是平行四边形，
∵点E是BC的中点，
∴随着点C的运动，点E在以OB为半圆的圆弧上运动，
当点C运动到弧AB的中点，点E运动的弧长=$\frac{90π•\frac{1}{2}r}{180}$=$\frac{1}{4}π$r．

点评 本题考查了切线的判定和性质，相似三角形的判定和性质，平行线的性质，列函数解析式，求弧长，正确的作出辅助线是解题的关键．