题目内容
7.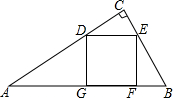 如图,∠ACB=90°,四边形DEFO为正方形,且四个顶点D,E,F,G在三角形ACB的边上.求证:FG2=AG•BF.
如图,∠ACB=90°,四边形DEFO为正方形,且四个顶点D,E,F,G在三角形ACB的边上.求证:FG2=AG•BF.
分析 根据正方形的性质得到DG=GF=EF,∠DGF=∠EFG=90°,由邻补角的性质得到∠DGA=∠EFB=90°,根据余角的性质得到∠ADG=∠B,推出△ADG∽△BFE,根据相似三角形的性质得到$\frac{AG}{DG}=\frac{EF}{BF}$,得到DG•EF=AG•BF,等量代换即可得到结论.
解答 证明:∵四边形DEFG为正方形,
∴DG=GF=EF,∠DGF=∠EFG=90°,
∴∠DGA=∠EFB=90°,
∵∠C=90°,
∴∠A+∠ADG=∠A+∠B=90°,
∴∠ADG=∠B,
∴△ADG∽△BFE,
∴$\frac{AG}{DG}=\frac{EF}{BF}$,
∴DG•EF=AG•BF,
∴FG2=AG•BF.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
15.一段斜坡公路的坡度为i=1:2$\sqrt{2}$,这段公路长为150m,则从坡底到坡顶这段公路升高( )
| A. | 75m | B. | 50m | C. | 75$\sqrt{2}$m | D. | 50$\sqrt{2}$m |
2.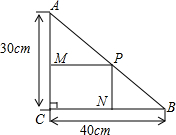 如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )
如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )
 如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )
如图,在Rt△ABC的内部作一个矩形CMPN,其中CM、CN分别在两直角边上,设CM=xcm,那么CN的长为( )| A. | 40-$\frac{4}{3}$x | B. | 40-$\frac{3}{2}$x | C. | 30-$\frac{4}{3}$x | D. | 30-$\frac{3}{4}$x |
12.市场调查显示,每年深圳体育中考前几个月,某种品牌的跑鞋将会热销.某公司为了抓住这一商机,决定进一批这种品牌的跑鞋,该公司对某中学初三学生的鞋码进行了调查,你认为该公司最关注的是这一组鞋码的( )
| A. | 中位数 | B. | 平均数 | C. | 众数 | D. | 加权平均数 |
19.下列各组中两个式子的值相等的是( )
| A. | 32与-32 | B. | (-2)2与-22 | C. | |-2|与-|+2| | D. | (-2)3与-23 |
16. 如图,在⊙O中,∠AOB=50°,则∠ACB=( )
如图,在⊙O中,∠AOB=50°,则∠ACB=( )
 如图,在⊙O中,∠AOB=50°,则∠ACB=( )
如图,在⊙O中,∠AOB=50°,则∠ACB=( )| A. | 30° | B. | 25° | C. | 50° | D. | 40° |